Getting Squared Away

Confession

Playing with numbers is one of my favorite ways to pass time. Of course, we can get to numbers per se in a variety of ways. One can be from simply doodling on a page. I remember drawing grids of dots on a page and playing all kinds of games with my classmates when I was in school. I’d like to say that this was only during breaks or free periods, but I know I won’t be able to pull the wool over your eyes, at least in this regard. Those of you who know me personally also know the glint that appears in my eyes when I am up to no good. Oh well!

As the well known saying goes, “An idle mind is the devil’s workshop.” And I often found myself bored stiff in many of my classes. In some of them I did take a perverse pleasure in disrupting the class. This was in classes where I had some kind of antagonism toward the teacher. But in other classes, where I found the teacher likable, I would engage in my random play, one kind of which was drawing grids and either contriving new games to play on the grid or discovering intriguing patterns.

Anyway, during my dot grid days I would attempt to come up with different types of grids. And of course, as mentioned earlier, I had to count the number of dots and recognize patterns. It was only much later that I realized that my (successful) efforts at distracting myself in some classes were actually leading to a common recreational mathematics idea – the centered square numbers. Let me explain.

Introduction to Centered Square Numbers

The centered square starts with a single dot. Each successive centered square is obtained then by surrounding the existing centered square with another layer of dots to complete a new square. The first four members of this sequence are shown in the figure below.

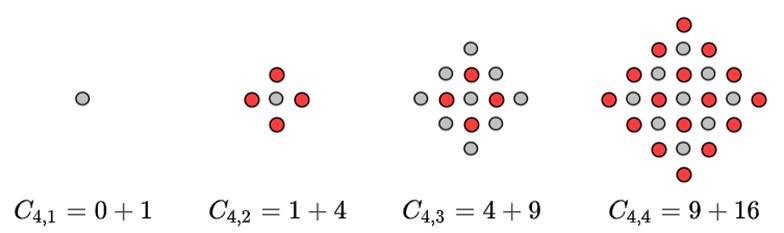
Allow me to explain the notation. In the term C_4,3, the ‘4’ refers to the number of sides in the regular polygons we are dealing with. In this case, since we are considering centered squares, the first number is a ‘4’, indicating a quadrilateral. The ‘3’ refers to the third member in the sequence. The C indicates the count of the number of dots.

In the figure, apart from the first member, each figure has both red dots and grey dots. If you focus on either the red or gray dots, you will notice that the set of dots of that color form a square. So in the third member, the red dots form a square of side 2 dots while the gray dots form a square of side 3 dots. Similarly, in the fourth member, the gray dots form a square of side 3 dots and the red dots form a square of side 4 dots. This is what is indicated on the right side of each equation. For the third member, 4 is the number of dots in a square of side 2 while 9 is the number of dots in a square of side 3. Similarly, for the fourth member, the square of side 3 has 9 dots while the square of side 4 has 16 dots.

We can now add the numbers on the right side of the equations to get

From this it is clear that the number of dots in the n^th member is equal to the sum of the squares of n and n – 1. Hence, we can write

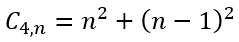
Fruits of Algebraic Massaging

With a little bit of algebraic ‘massaging’ we can show that

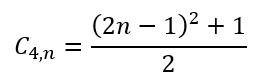
What this tells us is that the n^th centered square number is equal to half the sum of the square of the n^th odd number and 1. This can be illustrated as in the diagrams below:

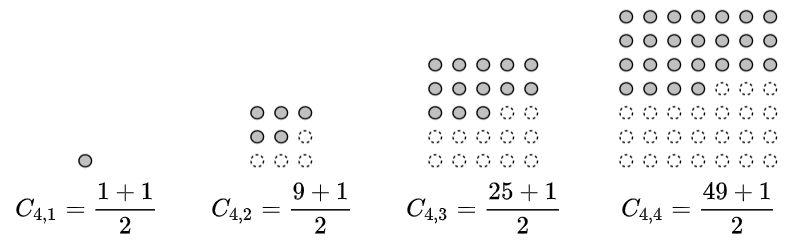
Here the dots in gray indicate the count for the centered square while the total number of dots is the square of the n^th odd number.

We can also ‘massage’ the expression for C_4,n as follows:

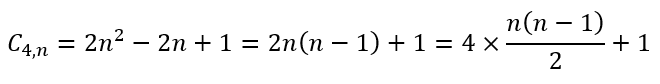
Now, if we consider the sum of the first n – 1 natural numbers we can see that

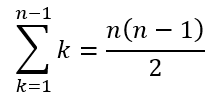
This means that the n^th centered square number is one more than four times the sum of the first n – 1 natural numbers. We can depict this as follows:

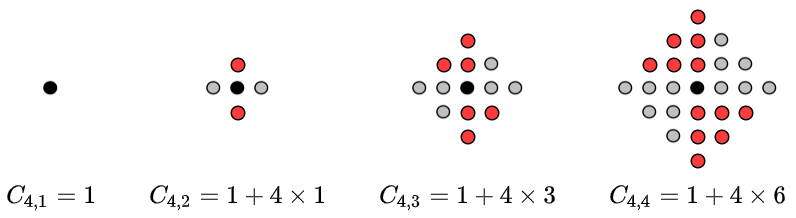
Here, the central black dot represents the 1 that is added at the end. The remaining dots are divided into 4 triangles, 2 in gray and 2 in red. Each of these triangles represents the sum of the first n – 1 natural numbers.

Further, since

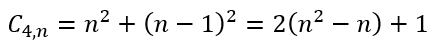
we can conclude that each centered square number is necessarily odd. We could obtain this intuitively from the fact that the centered square number is the sum of consecutive square numbers. Since one number must be odd and the other even, this must mean that we are adding an odd number, since the square of an odd number is odd, and an even number, since the square of an even number is even.

Of course, given the m^th odd number, we can obtain

This means that the square of an odd number is always 1 more than a multiple of 4. This leads easily to the conclusion that all centered square numbers are 1 more than a multiple of 4. This was depicted in the previous diagram since there are 4 identical triangles and the single black dot.

Absolution

As I played around with the grid of dots in my early days, I did recognize some of these patterns. Not all, of course. But it was quite intriguing that the simple endeavor of making a grid of dots could yield so many interesting properties. This began out of boredom in the classroom. I am confident that countless many of the discoveries and inventions we now know about and enjoy had their beginnings in the boredom of a child in a class he/she was forced to attend. If this is the case, I think I can be absolved for my boredom fueled explorations!