Last Call on the Whirligig

Forms of Complex Numbers

In the previous post, The Tripartite Fugue, we finally obtained the exponential form for complex numbers. As mentioned in the previous post, we will conclude our series on complex numbers today. Here I wish to explore a couple of aspects of complex numbers that become evident from the exponential form. I also wish to relate the rotational aspect of complex numbers to the idea of negation that we saw in A New Kind of Number?.

Let us begin our final exploration by reminding ourselves of the three equivalent forms for complex numbers we have obtained. So far we have

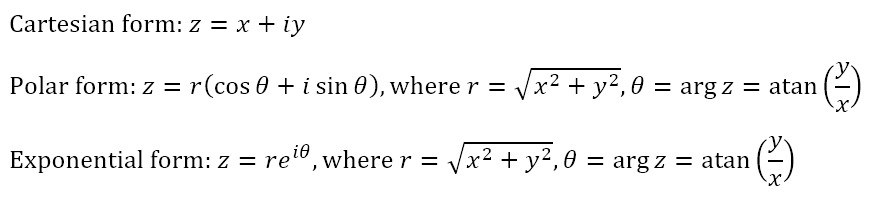
In the polar and exponential forms we recognize that, due to the periodicity of the trigonometric functions and fact that θ represents a rotation, there are infinitely many values of θ that, when used in the polar or exponential forms, could give us the same complex number.

Addition of Complex Numbers

Now, let us consider two complex numbers

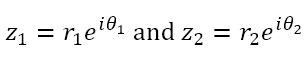
In polar form these would be

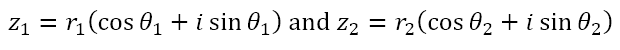
If we attempt to add the two complex numbers we would obtain

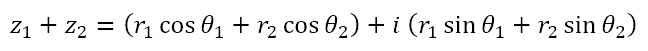
Special Case 1: r₁ = r₂ = r

Now, there is very little we can do to simplify the above. However, if we have the case where both complex numbers have the same modulus r, we can get

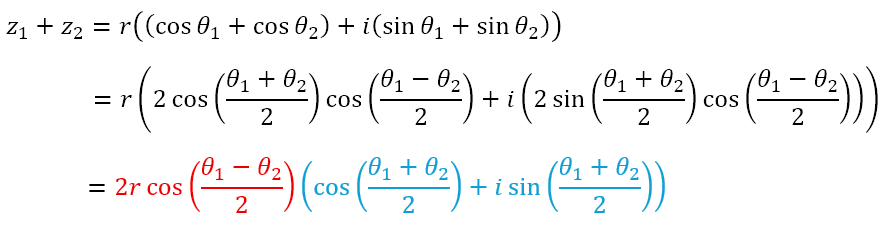
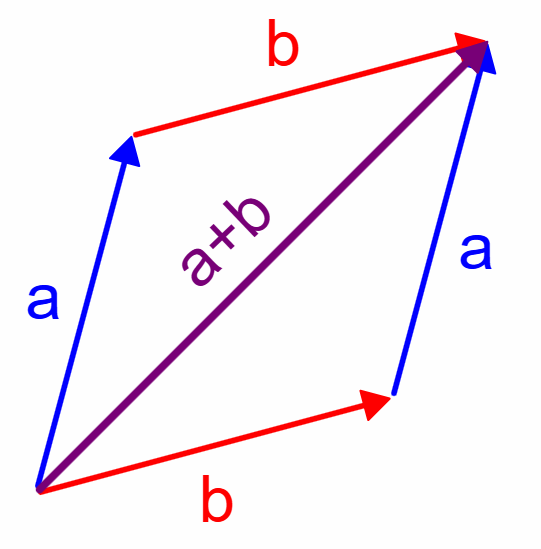
Here, we can recognize that the term in blue is a pure rotation, which must mean that the term in term gives us the modulus of the resultant complex number. Now, if we step back and think about what this represents, we can see that the two complex numbers z₁ and z₂ form adjacent sides of a rhombus, one inclined at θ₁ with the real axis and the other at θ₂. Quite obviously, the addition of the two gives us the complex number represented by the diagonal, which must bisect the angle between the two sides, meaning that it must be inclined at an angle of (θ₁ + θ₂)/2 with the real axis. Further, it is easy to show that this diagonal must have a length equal to the red term, where the angle (θ₁ – θ₂)/2 is that between one side of the rhombus and the diagonal.

Multiplication of Complex Numbers

Now, suppose we were attempting to multiply the original complex numbers. In exponential form they were

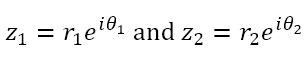
In polar form they are

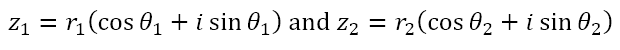
Using the polar form, we can obtain

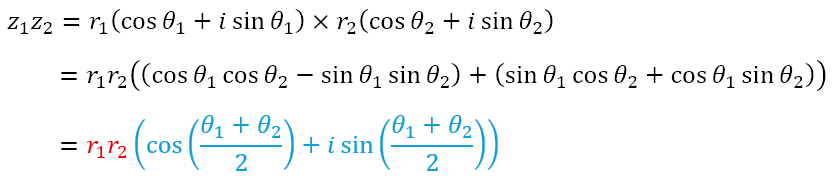
Once again, we can see that the term in blue represents a pure rotation, meaning that the term in red must be the modulus. Hence, when we multiply two complex numbers, their moduli get multiplied while their arguments get added.

This feature is much more easily recognized when we consider the exponential form since

Hence, if we consider z₁ to be our original complex number, then multiplying it by z₂ represents a further rotation by θ₂ and an enlargement by a factor of r₂.

Special Case 2: r₁ = r₂ = 1

Now, if we consider the case where the modulus of both complex numbers is 1, then we have a situation of pure rotation since any power of 1 is 1. So, there is no enlargement anymore, only pure rotation. Now,

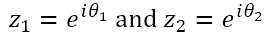
Hence,

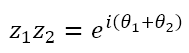
As we can see, since the moduli of both complex numbers is 1, the product represents only a rotation.

Special Case 3: r₁ = r₂ = 1, θ₂ = π

Suppose now that the second argument (i.e. θ₂) is equal to π. Then,

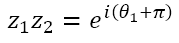
Per our understanding of rotation, this represents rotating z₁ by π radians in the counterclockwise direction. However, consider

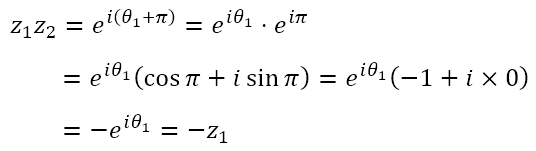
In other words, rotating a complex number by π radians in the counterclockwise direction, which is what e^iπ represents, is the same as negating a complex number. We saw the same thing when we considered real numbers in A New Kind of Number?. That is, we said that negating a real number can be thought of as a rotation by π radians. Of course, in that post, we hadn’t yet introduced the radian measure. Hence, we had said that negation is the same as a rotation by 180°.

We can solidify this understanding of negation by considering e^iπ using the polar form. Hence, we have

We saw this identity in The Eye of the Beholder, one of the first posts in this blog. In a different form, namely

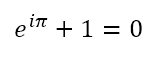
this is known as Euler’s identity.

Special Case 4: r₁ = r₂ = 1, θ₁ = 0, θ₂ = π/2

But if a rotation by π radians is equivalent to negation, what would a rotation by half of π radians be equivalent to? Here, I am intentionally choosing z₁ to be a purely real number so that we can see the effect the rotation has. Now,

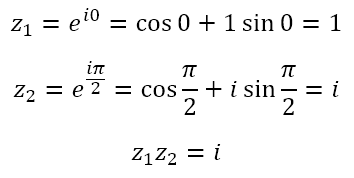
What this tells us is that the imaginary unit i represents a rotation in the counterclockwise direction by π/2 radians. We also know that i² = -1, which would correspond to two rotations of π/2 radians in the counterclockwise direction, which is equivalent to one rotation of π radians in the counterclockwise direction as we have just seen. Moreover, i³ = –i, which would correspond to three rotations of π/2 radians in the counterclockwise direction (i³), which is equivalent to one rotations of π/2 radians in the clockwise direction (-i).

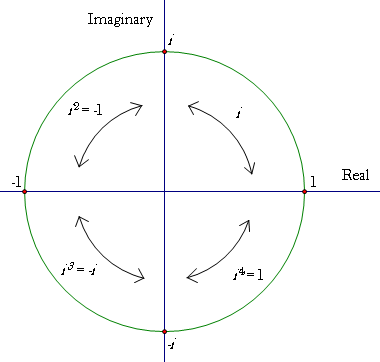
Significance of Rotation by π/2 radians

Of course, right away we should be able to see some sort of symmetric beauty in this. Each rotation through π/2 radians in the counterclockwise direction represents moving from one term to the next in the cyclic pattern 1, i, -1, –i, 1, i, -1, –i, … It also communicates that a rotation through π/2 radians in the counterclockwise direction represents a shifting of the weights (i.e. relative magnitudes) of the real and complex parts of a complex number. What do I mean? Consider

This is equivalent to

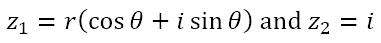
Now, when we multiply the two we get

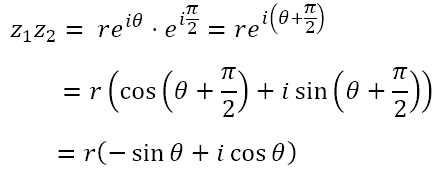
So we can see that, apart from any changes in ‘sign’, positive to negative or vice versa, the sine and cosine interchange positions. In other words, when we rotate by π/2 radians, the real and imaginary parts of a complex number exchange places. Much in the same way as multiplication by -1 changes the sign of a real number by negating it, rotation by π/2 radians involves moving what is real to become imaginary and what is imaginary to become real.

A Pedagogical Note

If you recall (and you probably don’t), in Primer to Complex Numbers, I had stated that it is unfortunate that we have used the terminology ‘complex numbers’. In A New Kind of Number? I stated that using the term ‘imaginary numbers’ is also unfortunate. This latter term is particularly unfortunate. Indeed, I have come across colleagues, that is mathematics teachers, who tell their students that the ‘imaginary numbers’ do not exist. Presumably, they mean that these numbers are like ‘imaginary friends’! However, these numbers are not figments of our imagination.

However, consider the Schrödinger equation shown below

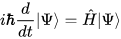
It is clear that the left side of the equation has the imaginary unit i. However, this equation represents a description of the evolution of the wave function of a non-relativistic quantum-mechanical system. In other words, the equation describes a very real physical phenomenon. Could this be possible if one side of the equation represents something that does not exist? In a similar way, Fourier analysis, which is used in signal processing, depends on the use of complex numbers. Finally, the Euler-Lagrange equations, a system of second-order differential equations, are the basis of Lagrangian mechanics, a way of describing motion using energy rather than forces, which are used in Newtonian mechanics.

I cite the above applications in physics precisely to show that complex numbers are essential to our ability to describe real world phenomena, which would be quite unthinkable if the ‘imaginary numbers’ did not exist. It is unfortunate that René Descartes’ prejudices against such numbers continues to misinform many teachers and, consequently, their students concerning these numbers.

Hence, when I teach this topic to my students, I prefer to all these numbers ‘non-real’ numbers with the prior definition, which I would normally give them, that “a real number is a number whose square is non-negative,” thereby leaving open the possibility that there could be numbers whose squares are negative.

Turning the Corner

And with that we wrap up our exploration of complex numbers. We have been at it since late January with a one week break for Good Friday and a three week hiatus for my grading assignment. During this series, we took a pit stop for trigonometry and another for calculus. Today, we saw how all of this relates back to a seminal idea with which I began this blog. It has been a whirlwind for me and I am sure you feel the same. So, in the next post, we will move in a different direction. Till then, keep it complex.