Circular Family Values

We are in the middle of a series on conic sections. We started with Finding Refreshment in the Desert, in which I introduced us to what a conic section is and demonstrated that the general second degree equation in two variables represents a conic section. After that, in Circular Tangentiality we obtained the general equation of a circle and derived the equation of the tangent to a circle at a point. Last week, in Contacting Circular Polarity, I introduced us to the concepts of the chord of contact and polar of a point with respect to a circle. And toward the end of the post I teased the reader with a mention of a ‘family of circles’. Whatever could that be?

Recall that the equation of a circle with center at (p, q) and radius r is given by

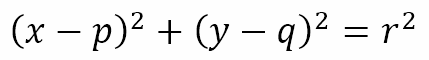
When this is expanded and rearranged, we get

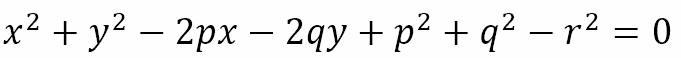
Recall also that the general second degree equation in two variables is

We can see that the equation of the circle is similar to the general second degree equation in two variables with

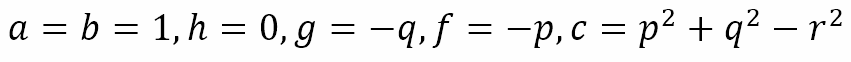
Hence, by convention we say that the general equation of a circle is

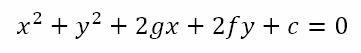
with center at (-g, –f) and radius given by

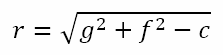
Now, suppose we are given the circles

The radical axis of these two circles is obtained by equating C₁ and C₂. Hence,

This is clearly the equation of a straight line and we can easily show that it is perpendicular to the line joining the centers of C₁ and C₂. Now consider the equation

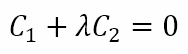
When λ = -1, this represents the radical axis. However, when λ ≠ -1, we can write the equation as

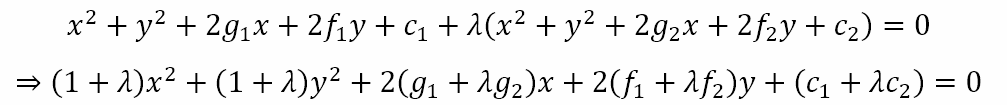
Dividing the equation by 1 + λ we get

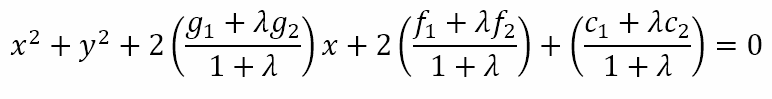
This clearly is the equation of a circle. Hence, by varying the value of λ we can obtain different circles. Suppose we attempted to find the radical axis of this circle and C₁. We would get

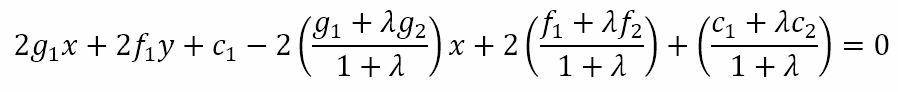
If we focused on the coefficient of x we would obtain

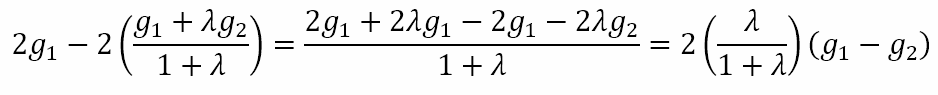
Hence, the equation of the radical axis would be

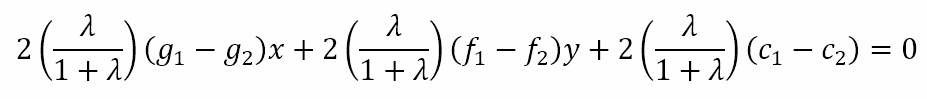
If we divide this equation by λ/(1 + λ) we will get

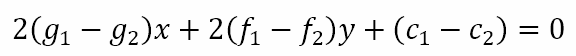
which is the radical axis of C₁ and C₂. In other words, any two members of this family of circles shares the same radical axis as the two circles used to generate the family.

While the study of family of circles began, as is the case for many concepts related to conic sections, simply as an exercise of playing with the mathematics, this obscure concept has found applications in the study of paths of light and designs of tires and gears. This has been the case with many mathematical concepts that were developed without any practical applications in mind. However, as the study proceeds, quite often unforeseen applications become possible.

There is much more that can be discussed related to the circle, even related to families of circles. However, that will take us really deep down this rabbit hole. Hence, we will leave the circle for now. In the next post, we will turn our focus to the parabola and see what properties this conic section has.