Contacting Hyperbolic Polarity

Brief Recapitulation

In this post we continue with the series on conic sections. In the previous post, A Mathematical Exaggeration, we introduced the hyperbola and derived the equation of the hyperbola in standard form. We also obtained the equations for the conjugate hyperbola, the auxiliary circle of the hyperbola and the equation of the tangent at a point on the hyperbola and the condition for tangency in terms of the gradient (m) of the tangent. In this post, we will explore the chord of contact and the polar with respect to the hyperbola.

Chord of Contact

Consider the hyperbola

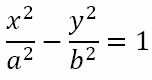
Recall that the equation of the tangent at the point (x₁, y₁) is

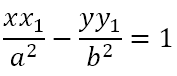
Let P(x₁, y₁) be a point outside the hyperbola

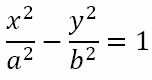
From point P tangents are drawn to touch the hyperbola at Q(x₂, y₂) and R(x₃, y₃). This is shown in the figure below.

Since PQ is the tangent at Q, its equation must be

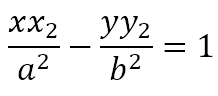
Since P lies on this tangent, its coordinates must satisfy the above equation. Hence,

Since PR is the tangent at R, its equation must be

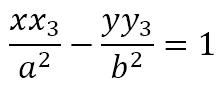
Since P lies on this tangent, its coordinates must satisfy the above equation. Hence,

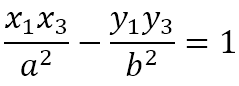
It follows then that Q(x₂, y₂) and R(x₃, y₃) satisfy the equation

Since two points determine a straight line, this must be the equation of the chord of contact QR.

Pole and Polar

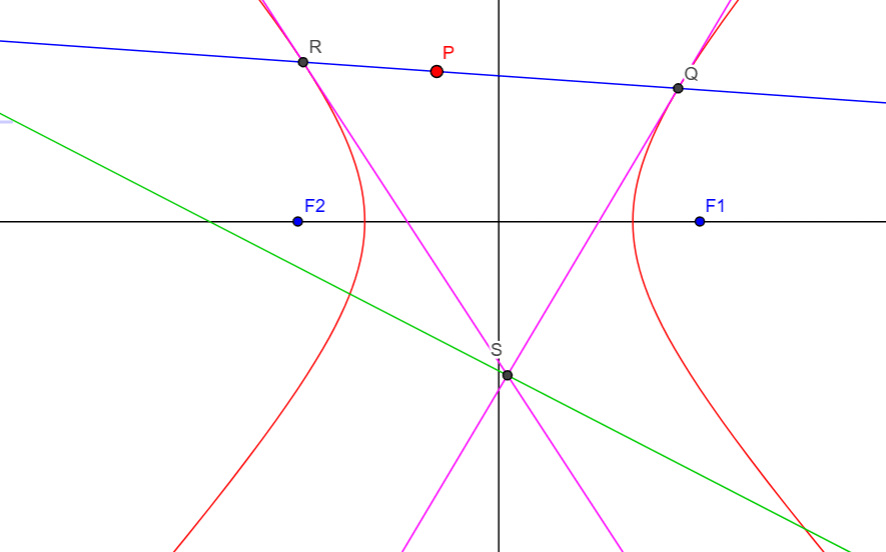
Having derived the equation of the chord of contact, let us proceed to derive the equation of the polar of a point with respect to the hyperbola. Let P(x₁, y₁) be a fixed point placed anywhere relative to the hyperbola. A line through P is free to pivot about P. In general, this line will cut the hyperbola at two points. Suppose these points are Q(x₂, y₂) and R(x₃, y₃). Tangents are drawn to the hyperbola at the points Q and R. Let these tangents intersect at S(h, k). This is shown in the figure below.

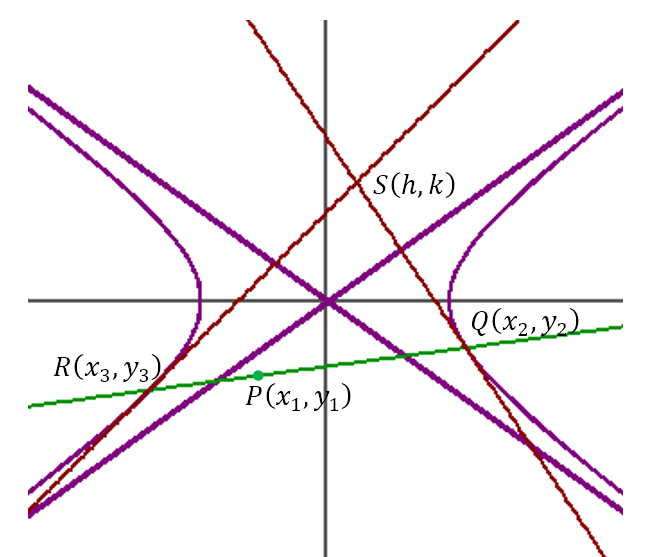
As the line through P pivots about P, the points of intersection of the line with the hyperbola will change. Hence, Q and R will move. This means that the tangents at Q and R will move. Hence, the point of intersection, S, of the two tangents will move. Then the locus of S is known as the polar of P wrt the hyperbola and P is known as the pole of the polar with respect to the hyperbola. It can be seen from the diagram that QR is the chord of contact of S wrt the hyperbola. Hence, its equation should be

However, P lies on QR. Hence, its coordinates should satisfy the above equation. This gives us

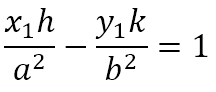
Generalizing, we obtain the locus of S to be

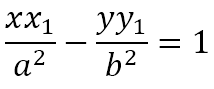
As just obtained, the polar of the point P(x₁, y₁) is

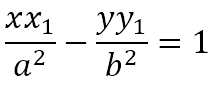
The point P(x₁, y₁) may be anywhere in relation to the hyperbola for a polar to exist. If the point P lies outside the hyperbola, the portion of it that lies inside the hyperbola is the chord of contact while the portion that lies outside the hyperbola represents the set of points actually reached by the polar. If the point P lies inside the hyperbola, the entire line represents the set of points actually reached by the polar for then there would be no chord of contact.

If you wish to see how the chord of contact, pole and polar relate to a hyperbola, you can click here for a Geogebra App that I created. There are two checkboxes on the top left. The upper one displays or hides the asymptotes of the hyperbola. More on this shortly. With the lower one unchecked, you can see how the chord of contact varies. Just click on the point P and drag it around! If you check the lower checkbox on the top left, you can explore how the pole and polar vary. Again, just click on the point P and drag it around to position the pole. I have made the line rotate automatically. This changes the positions of Q and R automatically and, therefore, the bright pink tangents at those two points. The point of intersection of these two tangents will move, tracing the green line, which is the polar.

The Asymptotes of a Hyperbola

An asymptote is a ‘tangent at infinity’ to a curve. In other words, as either the x coordinate or y coordinate or both increase in magnitude without bound, the curve gets closer and closer to the asymptote. While the parabola and hyperbola are both unbounded figures, only the hyperbola has asymptotes. For the hyperbolas

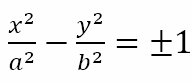
The lines

are the asymptotes. These are shown in the figure below

The ‘Inside’ of the Hyperbola

Now, observe the figure we have been using for the chord of contact and pole and polar.

By definition, a real chord of contact can be drawn only from a point outside the curve. Also, by definition, a chord must lie inside the curve. The chord of contact and the polar of  wrt the hyperbola is the green line. Since we are able to draw real tangents  PQ and PR, it follows that the point P lies outside the hyperbola but also that  lies inside the hyperbola! This is confusing so let us approach this differently.

The asymptotes divide the two dimensional space into 4 regions designated as shown below.

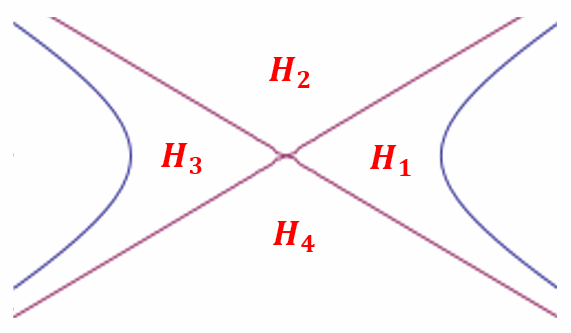
When the point P lies in a region H₁, the points of tangency will both be on the right branch of the hyperbola and the chord of contact will be ‘inside’ the right branch. When the point P lies in a region H₃, the points of tangency will both be on the left branch of the hyperbola and the chord of contact will be ‘inside’ the left branch. When the point P lies in a region H₂ or H₄, one point of tangency will both be on the right branch and the other on the left branch and the chord of contact will be ‘inside’ the two branches. Hence, the ‘inside’ of the hyperbola is a contextual idea that depends on where in relation to the asymptotes we place the point from which we desire to obtain the chord of contact.

The Hyperbola and Its Asymptotes

If we looked at the hyperbola and its asymptotes, we can see that the two asymptotes look much like a very ‘austere’ hyperbola with the two branches actually touching each other and the curved contours of the hyperbola becoming transformed into straight lines. It should come as no surprise, then, that, just as the circle is a degenerate form of the ellipse, the pair of lines that form the two asymptotes is a degenerate form of the hyperbola. Specifically, the pair of lines is a hyperbola with an eccentricity of infinity, much like the circle is an ellipse with eccentricity of zero. Indeed, the pair of lines has remarkable properties in and of itself, much like the circle did. And we will turn to that, the final ‘conic section, in the next post.