A Geometric Bifecta

Problem 1: Pure geometry

I recently came across two other interesting geometry problems, which I would like to tackle here. The first is depicted in the figure below.

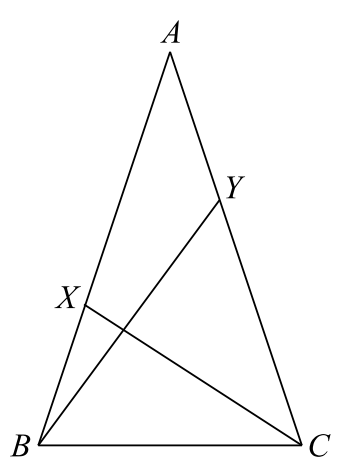
In the figure above, ΔABC is isosceles, with AB = AC and ∠A = 36°. Point X on side AB and point Y on side AC are chosen so that AX = BC = CY . Prove that BY and CX are perpendicular.

Given that the measure of ∠A is specified exactly and that the triangle is said to be isosceles, we should expect that both those factors of the problem will feature in the solution. We begin by observing that, if ∠A = 36° and ΔABC is isosceles, it must follow that ∠B = ∠C = 72°. But as soon as we say that, we also realize that 36 is half of 72. Could it be the case that CX actually bisects ∠C? Let us attempt to approach this by assuming that CX does not bisect ∠C. In that case, there must be another point Z on AB such that CZ bisects ∠C. This is shown in the figure below.

Now, if CZ bisects ∠C, then it follows that ∠ZCB = ∠ZCA = 36° = ∠A. Hence, in ΔZCA, ∠A = ∠ZCA, meaning that ΔZCA is isosceles, allowing us to conclude that CZ = AZ.

Now, ∠BZC is an exterior angle of ΔZCA. This means that its measure is equal to the sum of the opposite angles. Hence, ∠BZC = ∠A + ∠ZCA = 36° + 36° = 72° = ∠B. Hence, in ΔBZC, ∠BZC =∠B, meaning that ΔBZC is isosceles, allowing us to conclude that CZ = BC.

This means that AZ = BC. However, we are given that BC = AX. This can only be true if X and Z are the same point. Hence, we can conclude that CX bisects ∠C.

However, we are also given that BC = CY. Hence, ΔBCY is isosceles. But CX bisects the apex angle of this isosceles triangle, which means that it must be perpendicular to the base BY. And this concludes the proof.

Problem 2: Geometry and number theory

The second problem is depicted in the figure below.

In the figure above, the area of ΔABC is a whole number. Lines AX and BY are drawn, where X lies on side BC and Y lies on side AC, and these lines meet at point P, inside the triangle. The area of ΔBPX is 1, the area of ΔAPY is 2, and the area of ΔAPB is a whole number. Find the area of ΔABC, and prove that your answer is correct.

We begin by drawing the line PC and by labelling the regions as shown in the figure below.

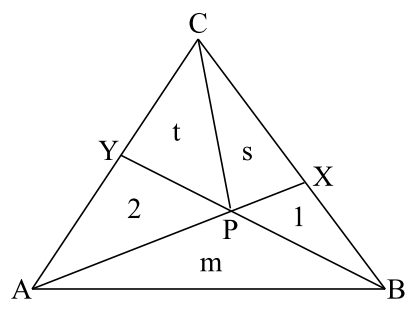
Hence, the areas of ΔABP, ΔPXC and ΔPY C are m, s and t, respectively, as indicated in the diagram. By hypothesis, m is an integer, and hence s + t is an integer, which we will call n. The ratio CX/BX is equal to the ratio of the area of ΔACX to the area of ΔABX, since the two triangles have the same height. This ratio is also equal to the ratio of the area of ΔPCX to the area of ΔPBX for the same reason. Hence,

Similarly, the ratio CY/AY is equal to the ratio of the area of ΔBCY to the area of ΔBAY, which is equal to the ratio of the area of ΔPCY to the area of ΔPAY. Hence,

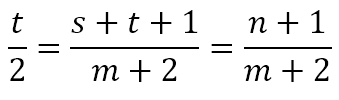
Now, since n = s + t, we can obtain

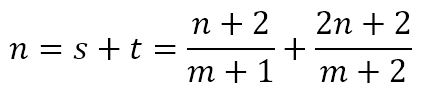
Some basic algebraic manipulations will give us

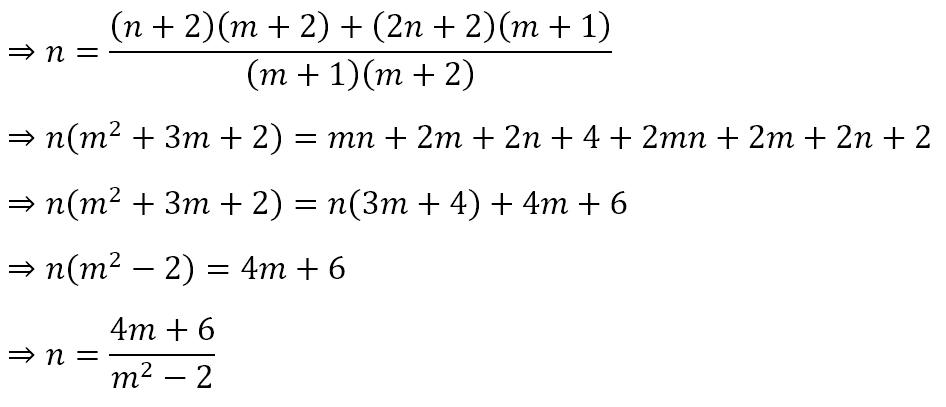
Now, since s + t = n is a whole number, we must have, n ≥ 1, which means that

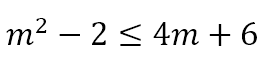
Rearranging this we get

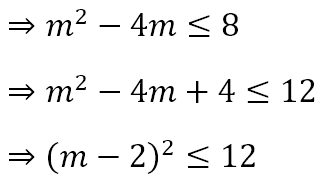
Since m is a whole number, we must have m is an element of the set {1, 2, 3, 4, 5}. The corresponding values of n are -10, 7, 18/7, 11/7, and 26/23. This means that the only solution is m = 2 and n = 7, allowing us to conclude that the area of ΔABC is 1 + 2 + 2 + 7 = 12.