Four Tangential Circles

This will be the final post for 2025. And it is a short one. I will be taking a break of a few weeks after that and will resume on 16 January 2026. For this final post, I would like to consider another problem I recently came across, depicted in the figure below.

Each of the four circles is tangential to the other three. Also, it is given that the radius of the largest circle is 2 units and the radii of the two identical circles is 1 unit. We are asked to determine the radius of the smallest circle.

As is often the case with geometry problems, a few simple constructions and a properly labelled diagram prove to be immensely helpful. These are shown below.

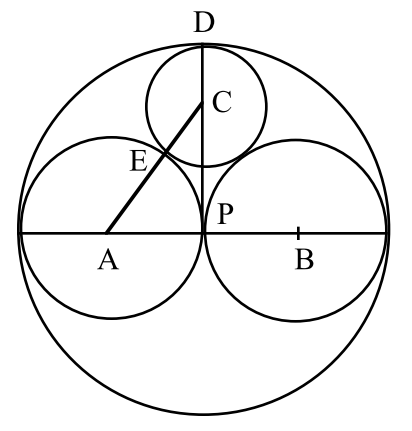
Here, A and B are the centers of the two identical circles and C is the center of the smallest circle. D is the point of tangency of the biggest and smallest circles. P is the point of tangency of the two identical circles. E is the point of tangency of the smallest circle and one of the identical circles. The points D, C, and P are collinear. Similarly, the points A, E, and C are collinear. Let the radius of the smallest circle be r.

Now, we know that AP = 1. AC = AE + EC = 1 + r. And CP = DP – DC = 2 – r. We can simply use Pythagoras’ theorem to obtain (1 + r)² = 1² + (2 – r)². This is trivial to solve as it yields a linear equation that gives r = 2/3.