Down for the Count

What Are Counting Principles?

Counting is something that we learn from a very young age, either in the informal environment at home or in the formal environment of school. It forms the basis of all the mathematics we learn through our lives. All the basic mathematical operations (addition, subtraction, multiplication, division, and exponentiation) can be explained in terms of counting. Hence, it is often the case that, when students reach high school, after probably 10 years of formal mathematics, they are surprised when they see a chapter in their book with the title “Counting Principles”. They may think, “What principles might this involve? How much more is there to counting? Didn’t we put the issue of counting behind us when we learned how to perform the operations?”

What the student does not realize is that what she has learned so far are ‘recipes’ for performing the mathematical operations. That is, she has been given some idea of what the operations involve. However, the main focus would have been on how to perform the operations not on why certain operations are needed to be performed. For example, if you were given 3 ⊗ 7, where ⊗ indicates some mathematical operation, what would the result be? 3 + 7 gives us 10, 3 – 7 would yield -4, 3 × 7 is 21, 3 ÷ 7 would be 0.428571…, and 3⁷ is 2187. While the student would easily be able to determine each of these five answers, which operation should she use in a given context? This is where the idea of the counting principles comes in. These principles tell us which operations are to be used in a given context.

The Multiplication and Addition Principles

As an example, suppose a restaurant offers a 3-course lunch with 3 options of starters, 5 of main courses, and 2 of desserts. How many different selections of lunch can a customer make? Or if you have a choice of a room from 3 hotels, one of which has 20 rooms, the second 30 rooms, and the third 50 rooms, how many choices of rooms do you have? How do the 3, 5, and 2 in the first situation relate to each other. How do the 20, 30, and 50 in the second situation relate to each other? There needs to be some principles on the basis of which the student would decide how to find the answer to each of the situations. What are these principles?

Today, we are starting a new series on counting principles. We will start with some basic ideas and work ourselves to more complex ideas. At the end we will answer the following question: “For a theatre production of a play there are n characters, each of which requires an understudy. If any of the actors and understudies can play all the parts and if the main actor must have more years of experience than the understudy, in how many ways can main actors and understudy actors be assigned?”

As promised, let us begin with the two earlier examples, which are relatively easy. Suppose we label the starters as A, B, and C, the main courses as P, Q, R, S, and T, and the desserts as Y, and Z. The possible choices are listed below:

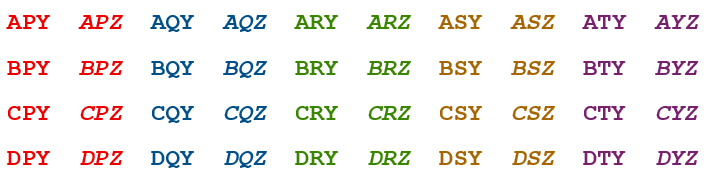
In the above, each row represents a different choice of starter. The colors differentiate the main courses. Finally, the dessert choice is differentiated between normal and italicized fonts. We can see that there are 40 possible selections because 4 × 5 × 2 = 40. But the reason we multiply is that the customer has to choose a starter and a main course and a dessert.

In the case of the hotels, we cannot multiply because the person can only occupy one room. Hence, he must choose to go to either hotel A, where he has a choice of 20 rooms, or hotel B, where he has a choice of 30 rooms, or hotel C, where he has a choice of 50 rooms, yielding a total of 20 + 30 + 50 = 100 choices.

The situation with the lunch choices is one in which we use what is known as the multiplication principle, while the case with the hotel rooms uses the addition principle.

The multiplication principle states that, if there are m ways of doing one thing and n ways of doing a second thing, then the number of ways of doing both things is m × n. The addition principles states that, if there are m ways of doing one thing and n ways of doing a second thing, then the number of ways of doing either thing is m + n.

Since the lunch menu required a choice of starter and main course and dessert, the multiplication principle was applicable. And since the hotel room required a choice of only one of the three hotels, the addition principle was applicable.

Your Turn

Why don’t you try the questions below?

1. A football squad consists of 3 goalkeepers and 5 strikers. In how many ways can the coach choose 1 goalkeeper and 1 striker?
2. A library allows members to borrow two books at a time. The library has 15 books by Jeffrey Archer and 23 books by Paulo Coelho. In how many ways can a member borrow 1 book by each author?
3. There are 5 apples and 7 oranges in a fruit basket. In how many ways can a person choose either an apple or an orange?
4. A student has 3 colleges to choose from. The first college has 3 programs, the second has 5 and the third has 6. Assuming that the programs are full-time programs, in how many ways can she choose a program?
5. A library allows members to borrow only one book at a time. The library has 15 books by Jeffrey Archer and 23 books by Paulo Coelho. In how many ways can a member borrow a book by either author?
6. Three cities A,B, and C are connected by 4 roads between A and B, 5 between B and C, and 6 between C and A. In how many ways can a round trip be made?

How did you fare with the above questions? The answers are 15, 345, 12, 14, 38, and 720. Many students get the first 5 but stumble on the last one. The answer I have given is correct. It is 720. If you wish to check the solution, click here.

Checking Out

As we continue with the series, we will see that there are many ways to put these two basic counting principles together. We will learn about permutations and combinations in the next post as well as the relation of the latter to Pascal’s triangle. We will also learn about how permutations and combinations relate to each other. We will also see why the combinations show up as the coefficients of the binomial expansion. Till then, let everything count.