The Eye of the Beholder

I was in the 12^th grade when I came across what I, along with many others, have come to recognize as the most beautiful equation in Mathematics. This was way back toward the end of 1986. Unfortunately, none of my Mathematics teachers that year ever bothered to show me and my fellow students the beauty behind this equation. Perhaps beauty is indeed in the eye of the beholder and my teachers had just not become beholden to the beauty that would eventually hold me.

It was while I was studying the topic of Complex Numbers that I came face to face with this mathematical beauty – elegant in its austere frugality and sensuous in its visual appeal. Unfortunately, it was many years later, when I was a Teaching Assistant at the University of Texas at Austin that my eyes were opened to this grand vision. As mentioned in my post on my motivations for starting this blog, I had to keep regular office hours. During the office hours many students used to visit me. But their questions pertained mainly to High School Mathematics rather than the Control Systems or Adaptive Control, for which I was TAing. Since both these courses required a heavy application of Complex Numbers, I had to really delve into the subject matter to be well prepared to address the questions the students might have had.

So I went back to the basics. I knew the rudiments of Complex Numbers of course. I could perform the four operations – addition, subtraction, multiplication, and division – on Complex Numbers. What more could there be? But when I went to self-study this topic, I realized that I wanted a hefty refund from the educational institutions I attended in the 11^th and 12^th! I had been thoroughly short-changed! It was as though someone had described the Sistine Chapel by telling me how Michelangelo had mixed his paints rather than tell me about the beauty of the actual frescos that he had painted on the ceiling!

Of course, Michelangelo could not have painted the frescos without knowing how to mix the paints. But mixing the paints wasn’t the goal! The purpose of mixing the paints was the beauty that be behold on the ceiling! Similarly, the purpose of studying Mathematics cannot be relegated to the success of its procedures. If it does not extend to the beauty of the subject students will not develop the skill of recognizing that austere and frugal beauty.

And so, not being satisfied with knowing how to mix ‘mathematical paints’ I allowed my ‘mathematical breath’ to be taken away by the beauty that these numbers held but that most students of Mathematics are just not introduced to at the time when the beauty can have the most impact on them – that is, when they are first learning about them.

Of course, the problem arises right when we first hear about these numbers. Almost without exception students will hear, if not learn, about these numbers in the context of learning how to solve quadratic equations. So the teacher will tell the students to consider the equation:

Here a couple of points about the notation above are needed. First,

tells us that a, b, and c are real numbers. While later study in complex numbers will get rid of this condition, it is needed at this stage to show the students that, even if we remain fully committed to using only real numbers, our solutions could end up being non-real. Second,

tells us that, in addition, a cannot be equal to 0. This ensures that we are actually dealing with a quadratic equation rather than a linear equation.

The teacher will then (hopefully) show the students that the solutions to the quadratic equations are:

Now the teacher will focus on the expression under the square root sign. It is called the ‘discriminant‘ and I was recently quite shocked to learn that many teachers have stopped telling the students this technical term. This is a travesty in my book! All areas of knowledge use technical terms that help communication between people working in those areas. Hence, to deprive students of the terminology and the reasons behind the terminology¹ is to deprive them of a robust education!

Anyway, the teacher will tell them that the ‘discriminant’ tells us something about the nature of the solutions. If the discriminant is positive, we get two real and distinct solutions; if it is zero, we get one real and repeated solution; and if it is negative, we get complex solutions.

Now quadratic equations are normally introduced in the 8^th or 9^th grade. Prior to this, the students would have learned some basic patterns for multiplication. Most relevant, in this context, is the fact that any non-zero number when squared yields a positive number. Inquisitive students will then probably ask the teacher how it can be that we can have a negative number under the square root because that would means that there are number, which when squared yield a negative number.

And here we encounter the first roadblock to the study of Complex Numbers. Remember, this question has arisen in the context of trying to solve an equations involving (presumably) only real numbers. We have ensured that a, b, and c are real. But the formula for the solutions raises the possibility that x could violate a consistent property of real numbers, namely that their square cannot be negative. So what kind of number when squared would yield a negative number? Unfortunately, the history of Mathematics itself proves to be a hindrance because these numbers were called ‘imaginary numbers‘. This unfortunate terminology has led many teachers of Mathematics to conclude that, since these numbers are ‘imaginary’ they must not exist, much like those voices in my head that I keep trying to silence!

The irony is that Mathematics gets increasingly abstract as it is. Still Mathematicians have compounded the problems students have with the subject by actually calling some numbers ‘imaginary’. If ever there was need for some prescient wisdom to reject the unfounded whims of René Descartes, it was certainly with respect to his derogatory use of this term! Unfortunately, the name has stuck and we are stuck with it.

The second roadblock to the student of Complex Numbers is the term ‘complex numbers’ itself! When most students already think that the subject is complicated enough, intentionally labelling an important class of numbers ‘complex’ is like shooting yourself in the foot!

Anyway, students are introduced to these ‘complex’ and ‘imaginary’ entities and have their phobias duly stoked. This is especially true if the teacher does not bother to communicate the beauty inherent in the concepts and focuses only on the procedures behind the operations on these numbers.

However, when I came across the equation I opened this post with and spent time with it, I realized that these numbers, far from being a figment of our imagination, which might be conveyed with the word ‘imaginary’, have a very tangible existence in the real world. Moreover, far from being complicated, as might be suggest by the word ‘complex’, these numbers actually enable the linking of parts of Mathematics that we might otherwise be led to think are unconnected.

I have hyped this equation a lot. And you may be thinking there is no way I can deliver on my promise. Let us see.

The equation that I have been referring to, of course, is:

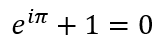
This is referred to as Euler’s Identity, another case of unfortunate terminology since identities normally contain variables and this equation has none!

So what’s so great about this equation? First, it contains three mathematical operations – addition (indicated by the ‘+’ sign), multiplication (hidden between the ‘i‘ and the ‘π‘), and exponentiation (the power of ‘e‘). Given that subtraction is just addition in reverse and division is multiplication in reverse, this equation contains all the basic mathematical operations. Second, it links the additive identity (i.e. ‘0’), the multiplicative identity and unit of real numbers (i.e. ‘1’), the base of the natural logarithms (i.e. ‘e‘), the number that describes the shape of a circle and the angle measure for a semicircle (i.e. ‘π‘) and the unit of imaginary numbers (i.e. ‘i‘). Third, the equation links arithmetic (indicated by the presence of ‘0’ and ‘1’), geometry (indicated by ‘π‘), growth (indicated by ‘e‘) and complex analysis (indicated by ‘i‘). The equation, of course, is a special case of a more general equation, known as Euler’s Formula, in which the links with trigonometry and calculus are also explicit. Fourth, the equation also links integers (‘0’ and ‘1’) with irrational numbers (‘e‘ and ‘π‘) and imaginary numbers (‘i‘). So many connections across so many concepts and branches of Mathematics, all contains in one single, simple equation with 7 mathematical symbols!

Unfortunately though, the High School Mathematics syllabuses in most countries divide the course content into almost rigid and impervious categories, isolated from each other. Since most of these syllabuses are artificially bloated to communicate the false notion of rigor, teachers scarcely have enough time to bulldoze through the syllabus. Stopping to smell the ‘mathematical roses’ is all but impossible. Hence, an equation that, in its simplicity and efficiency, demonstrates the inter-relatedness of all parts of Mathematics, thereby shattering the illusion that the various parts of Mathematics can – or God forbid are expected to – function in isolation from each other, should be one with which I believe teachers of High School Mathematics should become intimately familiar.

1. The expression is called the ‘discriminant’ because it allows us to ‘discriminate‘ concerning the nature of the solutions without having to solve the equation. ↩︎