What’s In A Name?

The Presenting Problem

There is one big problem with being a mathematics tutor. You aren’t the students’ main teacher and hence you get to hear what the students have actually learned from their main teacher. Why is this a problem? Well, it exposes me to the ways in which we mathematics teachers regularly let our students down. It is an indictment of the self and no one likes that.

Today, I wish to highlight one area in which we mathematics teachers often fall short – the area of terminology. I am a stickler for terminology. Technical terms in a field are essential for succinct and precise communication. Without these technical terms, we would have to use many more words. Not just that, when the number of words needed to refer to something increases, the possibility of paraphrasing also increases, thereby making the meaning dependent on the vicissitudes of the language in use. Hence, the communication becomes verbose and imprecise, leading to inefficiencies and possible lack of understanding. The use of correct terminology enables precise and succinct communication and facilitates understanding.

I am fed up, for example, of hearing students ask, “Do I minus the two?” Hello! Hello? What’s that? The word ‘minus’ is not a part of English grammar but a way of vocalizing the mathematical symbol that indicates subtraction. Similarly, hearing a student say that 1/x is the ‘inverse’ of x, has as bad an effect as it would have had if the student dragged his nails across the wall because there is a difference between an ‘inverse’ and a ‘reciprocal’. And finally, hearing a student tell me she wants to ‘bracket the terms’ when she means ‘factorize’ is pure agony.

Introduction to Nomenclature

I had a good early mathematics education. I don’t mean that all my mathematics teachers were capable teachers. I don’t remember most of them. And even the ones I remember weren’t all capable. But I remember being taught terminology from a very early age. While I do not remember ever using ‘addend’, ‘minuend‘, or ‘subtrahend‘, I clearly remember using ‘multiplicand‘, ‘dividend‘, ‘divisor‘, ‘quotient‘, and ‘remainder‘. The former set was probably never learned because addition and subtraction are covered very early. By the time multiplication and division were learned I guess I was old enough to learn bigger words.

But today I find that many students cannot recognize even the terms in the latter set. So instead of saying, “When you divide the dividend by the divisor, the result is the quotient with a remainder” we would have to say something like, “When you divide one number by another, the result is the largest number by which the second number should be multiplied without exceeding the first with the difference if any between the first number and the largest multiple of the second.” So instead of 16 words, in which most of the non-technical words are simply connectors of sorts, we would have to use 39 words, where many of the additional words describe the operation of division and the role of the different. And since others may phrase it differently, we would never be sure that we are communicating with accuracy.

Case in Point

One of the terms that causes me most pain is the ‘discriminant’. For those of you who do not know or do not remember or have conveniently suppressed the memory, when you attempt to solve a quadratic equation of the form ax² + bx + c = 0, the solutions are given by

Here the quantity under the radical sign (i.e. ‘√‘) is called the ‘discriminant’. Of late, many students come to me, having learned quadratic equations in grade 9 or 10, but having never heard the term. Why do I say this term is important? Because its name, like most mathematical terms, tells you what it does. The ‘discriminant’, you see, allows us to ‘discriminate’ between the kind of solutions a given quadratic equation has before we attempt to solve the equation. It can tell you if the equation has two different real solutions, only one real solution, or no real solutions. Give that this expression is so critical and that it is named to reflect what it does, a failure to teach students the term can only be viewed, at least according to me, as indicative of a failure of mathematics teachers to pass the baton of knowledge to the next generation. I even have textbooks written for high school students that do not have the term.

I can understand the reluctance that some teachers in the elementary school have concerning teaching some of the technical terms. Mathematical jargon can get to be quite heady. However, the failure to teach students these terms results in a lax approach to conversing about mathematics. However, even if we grant that many of these terms are too daunting to be taught in the elementary school, it is irresponsible to avoid teaching them at least in middle school.

Contextual Nomenclature

After all, soon after they enter high school, they will be introduced to contextual terminology. What do I mean? Consider the expression

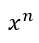
Most people who have done some middle school mathematics would be able to say that, in the expression above, x is the base. But what do we call n? When this notation is first introduced, it is called a ‘power’. Later, the students are told that it is an ‘index’. Still later, they are told to call it an ‘exponent’. And after they are introduced to functions and their inverses, they are told that n can also be called a ‘logarithm’. Four different terms for the same quantity! But mathematics is an austere field. It does not do ‘synonyms’! So why do we have so many ways of naming the same thing? It has to do with the context within which the quantity is being referred to. A student who understands the contextual naming of the quantity will also understand the reason behind it. In other words, by introducing the student to contextual terminology, we facilitate his/her fluency in mathematical discourse and depth of mathematical understanding.

Giving No Quarter

But someone may wonder why I am so adamant that teachers should consistently use and teach their students to consistently use correct mathematical terminology. After all, would not a rose by any other name smell just as sweet? Indeed it would! But no one goes around describing a rose. We choose a name by convention and use it so that everyone understands what we mean. Hence, since the mathematical community has landed on a set of naming conventions, it behooves teachers to teach their students that convention of nomenclature.