A Convention of Collaboration

Inane Phrases

If you read my motivations page and the previous post, you will realize that my experience of teaching grade 6 students had an immense impact on me. While the previous post focused on BEDMAS (or BODMAS or PEMDAS, etc.), in the motivations page I also reveal that the students came to me with what I said were “some inane phrases to remember while performing operations.” Unfortunately, I have found these inane phrases all to prevalent even among students in high school.

You may be wondering what these inane phrases are. Well, for instance, you may hear a student say, “Minus and minus equals plus” or “Minus and plus equals minus.” Another student may say, “Positive and positive gives positive” or “Positive and negative gives negative.” Whatever in the world is this nonsense?

Most of you might, however, know what they are trying to say. However, without any proper context within which the phrases are to be interpreted, I could conclude, as many students do, that – 2 – 3 = +5. After all, “minus and minus equals plus,” right? Or I could insist that – 7 + 10 = – 3 since “minus and plus equals minus.”

Need for Precision and Clarity

What the phrases actually intend to communicate are “the product of two positive numbers is a positive number,” “the product of two negative numbers is a negative number,” and “the product of a positive number and a negative number is a negative number.” Of course, my phrases have 10, 10, and 14 words, while the original inaccurate phrases have 5 words each. The inaccurate phrases are certainly more economical in terms of the number of words they contain and the time it takes to say them. And don’t get me wrong. I’m all for saving time and effort.

However, I am not for saving time and effort at the cost of precision and accuracy and clarity. If the price exacted by the shorter phrases is the confusion among students about whether these are applicable only for multiplication or also for addition and subtraction, then I think the price is too high to pay.

Basic BEDMAS

But you may ask, “If these phrases are applicable only for multiplication, what rules do we follow when it comes to addition and subtraction?” This is a valid question because here too I have found students floundering. It’s not just that they have got the order of operations wrong, but also that they do not understand what is happening, especially when we are asked to add and subtract multiple numbers, some of which are positive and others of which are negative.

Let us consider one problem. Suppose we are asked to evaluate

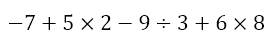
Equipped with our understanding that the convention is to perform division and multiplication first, we obtain

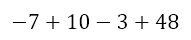
Now what do we do? We begin by performing the calculations from left to right. What we first do is orient ourselves so we imagine we are on the number line facing the right (i.e. the positive direction). Now, we locate ourselves where the first number is. So we land on the position for -7.

Now all we have to do is move forward or backward the appropriate number of steps according to whether we encounter an addition or subtraction respectively. So, we first move forward 10 spaces, landing on +3, then back 3 spaces, landing on 0, and then forward 48 spaces, landing on +48.

BEDMAS with the Brackets

But what if we have something more complicated, say something that involves brackets? Consider the following

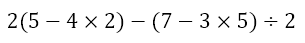
Here we have two separate parentheses to deal with. Since both are unrelated, in that there is a subtraction operator between the two, we can deal with both simultaneously. So we can first obtain

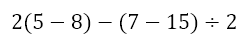
We can now complete our dealings with the parentheses to get

Now the –8 represents the negation of -8, which would give +8. Hence, we have

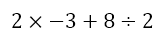
Now, the initial multiplication involves one positive number and one negative number, meaning that the product will be negative. The division involves two positive numbers and hence will yield a positive number. So we have

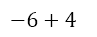
This gives the final answer as -2.

In the above example, we had obtained –8 and I stated that this was the negation of -8. We could have also considered

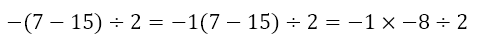
Here, instead of the negation of a negative number, we are considering the product of -1, which is inherent in the standalone negative sign, and -8, which gives us +8 since it is the product of two negative numbers.

BEDMAS ‘Brain Teasers’

Now, almost everyday I get some BEDMAS ‘brain teaser’ in my social media feeds. I don’t know why. Maybe my interest in mathematics related posts makes the idiotic algorithm ‘think’ that I would like such ‘brain teasers’. The reason I’m placing ‘brain teaser’ in inverted commas is because I do not think these problems qualify as brain teasers. They only check whether you know the rules of BEDMAS.

‘Brain Teaser’ 1

Anyway, one such ‘brain teaser’ is

We know we need to deal with the brackets first. To do this, we need to calculate 8 – 6 + 3, which equals 5. Hence, the problem reduces to

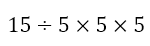
Since we only have multiplication and division with no grouping, we can proceed from left to right. This gives us

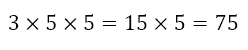
It is important to note that in the expression 5(8 – 6 + 3), we are not instructed to group the 5 and the value of the parentheses. Hence, the 5, which comes after the division sign, becomes the divisor, while the 5, which is the value of the parentheses, is a normal multiplicand.

‘Brain Teaser’ 2

How would we calculate the value of

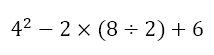
Here, we observe that there is a parentheses that we need to deal with first, yielding

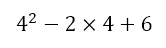
Now, we have an exponent, which we need to address next, giving us

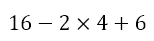
Now we have to perform the multiplication to get

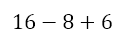
This leaves just addition and subtraction, which we can perform from left to right to get

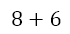
which yields 14 as the final answer.

‘Brain Teaser’ 3

But what if we have something like

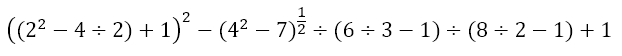
We recognize that the first term has a nested bracket. Hence, we need to first deal with the innermost bracket. This bracket contains an exponent, which we need to perform first. The second term has an exponent, which we will perform first in that term. The third and fourth terms have division, which we will perform at this stage. This gives us

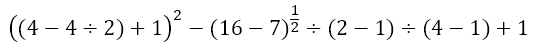
Now, we have to perform the division in the innermost bracket of the first term. At the same time, we can evaluate the brackets of the second, third, and fourth terms. This gives

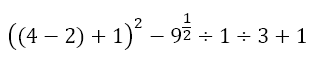
Now we can evaluate this innermost bracket of the first term. At the same time, we can evaluate the exponent on the second term. We now have

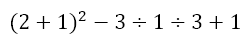
Evaluating the first bracket, we get

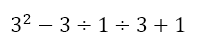
Now evaluating the exponent gives us

Observe that we have two division operators one after the other. When faced with this situation, we need to perform the operations one by one from left to right. So we first get

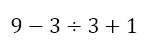
because the first division was 3÷1, which equals 3. Now we can perform the remaining division to get

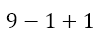
Now we have only addition and subtraction, which we can perform from left to right to give us 9 as the final answer.

It’s a Wrap

What we can see is that following the BEDMAS rules carefully will yield an unambiguous answer. As mentioned in the previous post, the is nothing sacrosanct about BEDMAS. It is not inherent to any of the operations. However, this is the convention that has been adopted by mathematicians so as to remove confusion and to ensure that any particular arithmetic calculation yields one and only one answer. In these two posts I hope I have communicated the rules of BEDMAS well enough for anyone at or above grade 4 to understand. I hope the examples I have given serve as good illustrations of the process. But more than that, I hope I have communicated the fact that BEDMAS is a convention that could only have been agreed upon if there was a spirit of collaboration and camaraderie among mathematicians.