A New Kind of Number?

The Discriminant Revisited

Last week I began a series on complex numbers with the post Primer to Complex Numbers. At the end of that post, I considered the discriminant in the formula for solving a quadratic equation. We saw that it is easy to comprehend what a zero or positive discriminant would mean simply because the square of zero is zero itself and the square of a positive or a negative number will always give a positive result. However, what do we do with quadratic equations in which the discriminant is negative?

Visualizing Quadratics vis à vis the Discriminant

Here, it would help for us to visualize the functions corresponding to the quadratic equations. In other words, given the equation

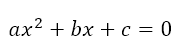
we can consider this to be the equation f(x) = 0, where

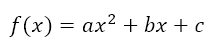
This is nothing less than finding the points where the graph of y = f(x) cuts the x axis. So, let us consider three different quadratic functions

If we plot the graphs of these functions we will get

We can factorize f(x) and g(x) giving us

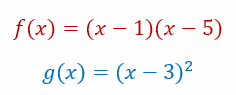
Here we can see that the factors x – 1, x – 5, and x – 2 correspond to the solutions of the corresponding equations f(x) = 0 and g(x) = 0. These also are the x-coordinates of the points where the graphs of y = f(x) and y = g(x) cut the x-axis. However, we can see that we cannot factorize h(x). Nor does the graph of y = h(x) cut the x-axis. If we calculated the discriminants of the three quadratics we would obtain

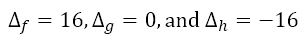
So, when the discriminant is negative, we can see that the graph of the corresponding quadratic function does not cut the x-axis. This is precisely what we mean when we say that the quadratic equation does not have real roots or real solutions.

However, if the quadratic equation does not have real roots, what kind of roots does it have? In other words, what kind of number can we propose which when squared gives us a negative number?

Reimagining Negation

Let us take step back and ask ourselves how we can visualize negating a number. What I was taught, and I think what most students today are taught, is that negating a number involves taking its reflection in the zero point. Hence, the negation of 4 is -4 and the negation of -3 is 3. We can visualize both of these as follows.

However, we can also visualize this as an anticlockwise rotation of 180° as below.

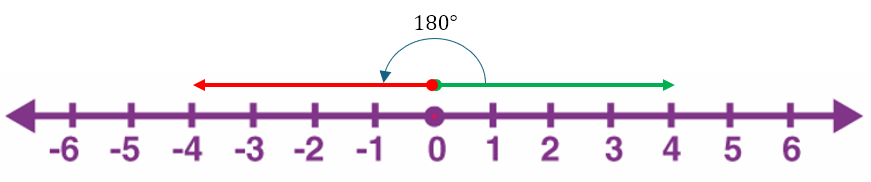
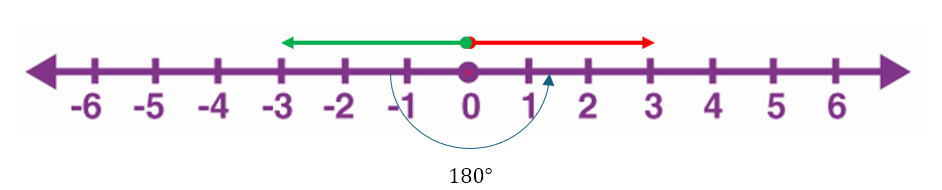
I will later drop the degree unit for measuring angles and replace it with the radian. I will also explain why I am considering an anti-clockwise rotation when we make this change. But for now, it should be clear that an anti-clockwise rotation about zero of 180° on the number line produces the same effect as negating a number.

We can now consider the positive sign to represent no rotation and the negative sign to represent a rotation of 180°. Then the product of two positive numbers will involve no rotation, that is, a positive sign. Similarly, the product of a positive and a negative number will involve no rotation and a rotation of 180°, that is, a negative sign. And the product of two negative numbers will involve two rotations of 180°. This will be a rotation of 360°, which is a complete revolution, or the equivalent of no rotation, yielding, once again, a positive sign.

So what if we considered the square root of a negative number to involve a rotation of 90°? In that case, the product of two such numbers would be two rotations of 90°, which equals an effective rotation of 180°, that is, a negative sign.

The Next Step

What we can see is that, if we are willing to ‘step out’ of the constraints of the number line by introducing the idea of rotations, then we can conceive of a way in which a ‘number’ which when squared gives a negative number. Of course, since we have ‘stepped out’ of the number line to understand these ‘numbers’, it is clear that these ‘numbers’ do not belong on the number line. And since the number line is intended to represent all ‘real numbers’ we are forced to conclude that these new ‘numbers’ are not ‘real numbers’. It is an unfortunate fact of mathematical history that these numbers were given the name ‘imaginary’.

In fact, it was the philosopher and mathematician, René Descartes, who rubbished the idea that there could be numbers whose squares were negative and who then jokingly called them ‘imagined’ numbers, that is, no more than a figment of our imagination. The name stuck. However, while it is great to have some historical humor in the nomenclature, there are many mathematics teachers today who actually think these numbers are entirely made up. As we will see in future posts, this is not the case. So, in the next post, we will look at understanding some arithmetic and algebra related to these numbers. Till then, let your imagination soar!