Deriving Derivatives – Part 1

Rewinding a Bit

We began our exploration of calculus last week with The Sky is the Limit. This is the second pit stop in our exploration of complex numbers. The first pit stop dealt with trigonometry. In the previous post we had looked at the idea of the limit, which I said was a central concept in the study of calculus. In this post I wish to obtain a few standard results that we will be able to use in our exploration of complex numbers.

In the previous post, we saw that the limiting value of the gradient of the secant through a fixed point on the graph of a function as another point approaches the fixed point is the gradient of the tangent at the fixed point. In the context of calculus, this is known as the derivative of the function at the point.

Definition of the Derivative

Suppose we have a function y = f(x). Then the derivative is denoted by

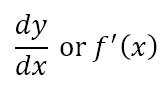
Per the limit definition of the derivative, we can say that

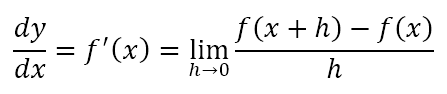
Note that the quantity inside the limit is simply the gradient of the secant at the point (x,f(x)). As h approaches 0 the gradient of the secant approaches the gradient of the tangent (i.e. the derivative) and the limiting value of the gradient of the secant is the gradient of the tangent.

Algebra of Differentiation

In what follows, u and v represent function of x.

The Sum Rule

The derivative of the sum of two functions is equal to the sum of the derivatives of the two functions. Symbolically, we state (u + v)’ = u‘ + v‘. This can be obtained as follows

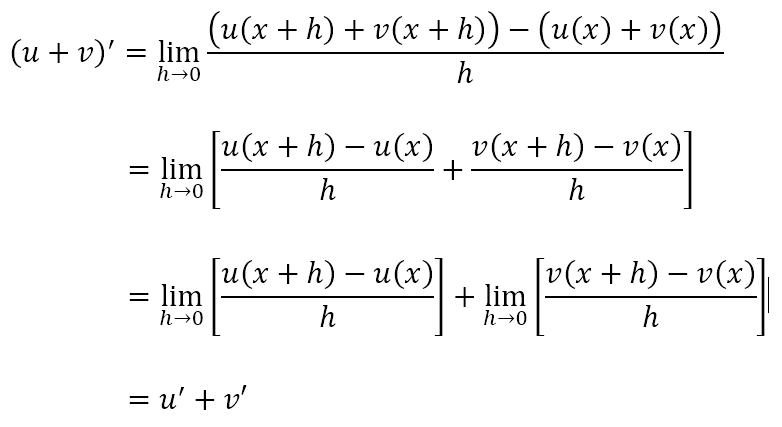
Difference Rule

The derivative of the difference of two functions is equal to the difference of the derivatives of the two functions. Symbolically, we state (u – v)’ = u‘ – v‘. This can be obtained as follows

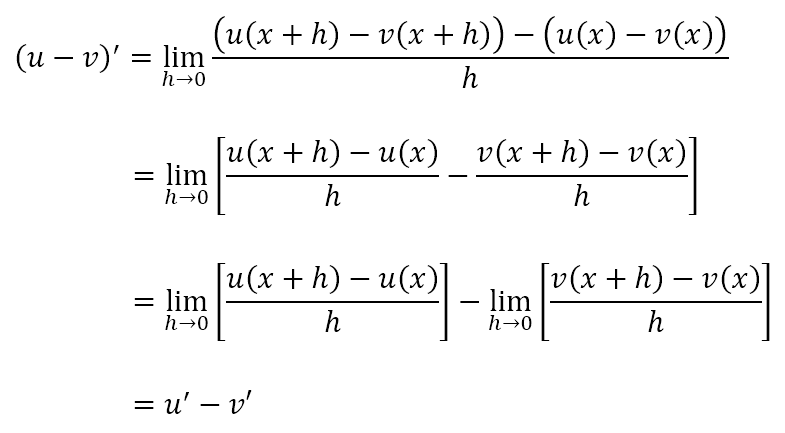
The Product Rule

The derivative of the product of two functions is equal to the sum of the product of the first function and the derivative of the second and the second function and the derivative of the first. Symbolically, we state (uv)’ = uv‘ + vu‘. This can be obtained as follows

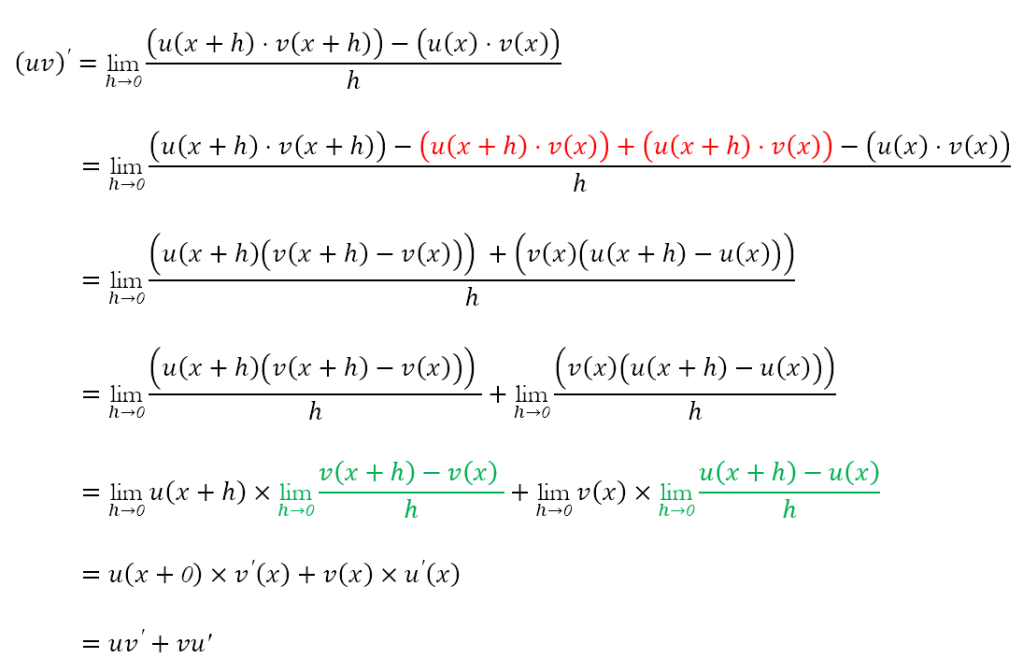
The Quotient Rule

The derivative of a quotient is equal to the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator divided by the square of the denominator. Symbolically, we state (u ÷ v)’ = (vu‘ – uv’) ÷ v². This can be obtained as follows

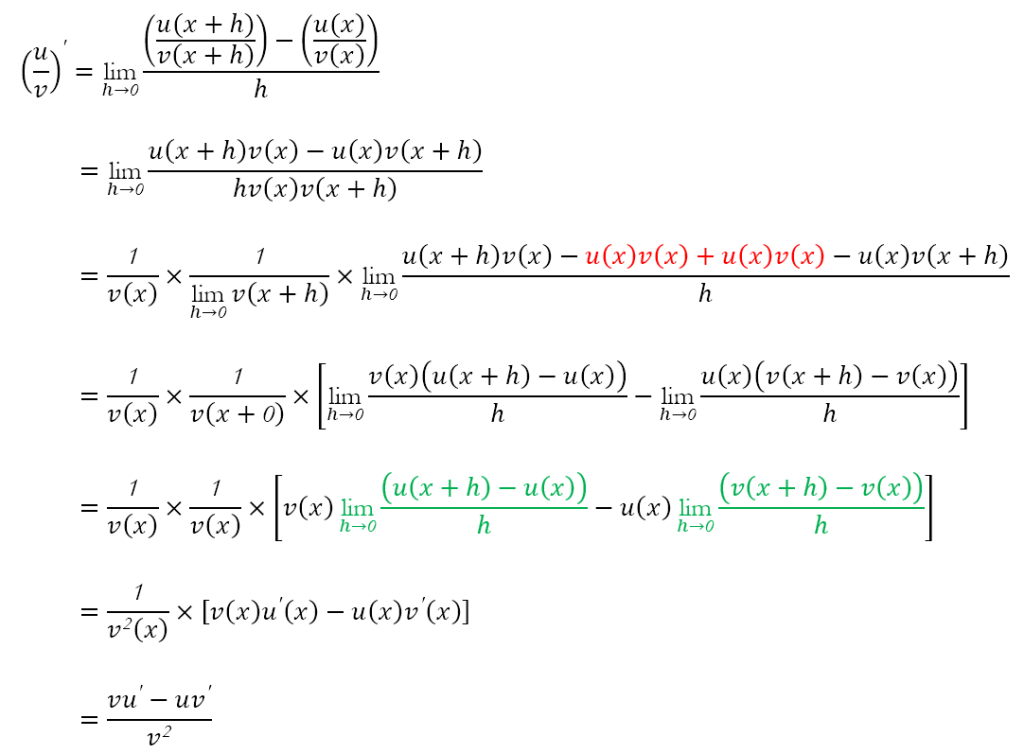
Derivative of xⁿ

Having obtained the results for the algebra of differentiation, let us derive our first derivative. Let us consider the function y = xⁿ. Per the definition of the derivative we have

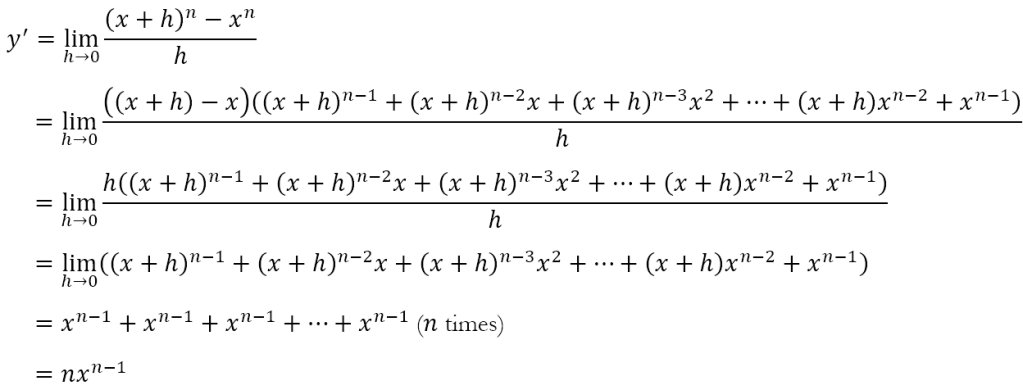
While I have only derived the result for positive integral values of n, the result can easily be obtained for all rational values of n. But what does this mean? Let’s take some concrete cases.

Suppose f(x) = x³. Here we can see that n = 3. Hence the derivative will be given by f'(x) = 3x². This means that, at the point where x = 2, the gradient of the tangent is f'(2) = 3(2)² = 12. Similarly, for the function f(x) = x^2/3, n = 2/3. Hence, the derivative will be given by f'(x) = (2/3)x^-1/3.

Derivative of sin x

Now, we have seen that the polar form of complex numbers involves the trigonometric ratios of the argument of the complex numbers. This means that it is quite likely that the derivatives of the sine and cosine functions will be needed in our further exploration of complex numbers. So let us obtain the derivative of the sine function. Suppose y = sin x.

Limit of sin x ÷ x as x → 0

Let us first obtain the limit of sin x ÷ x as x approaches 0.

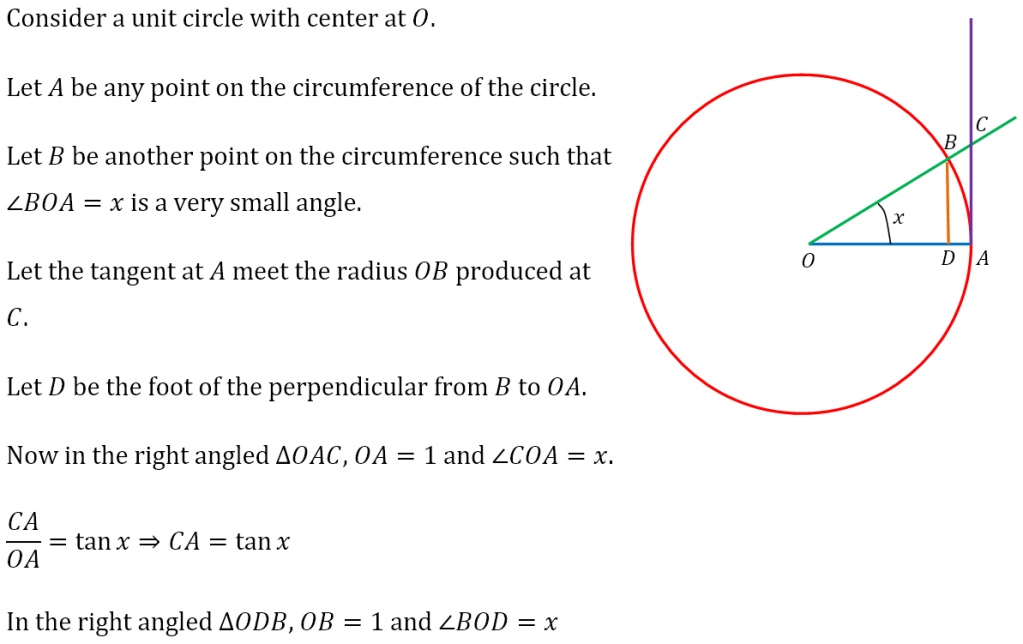
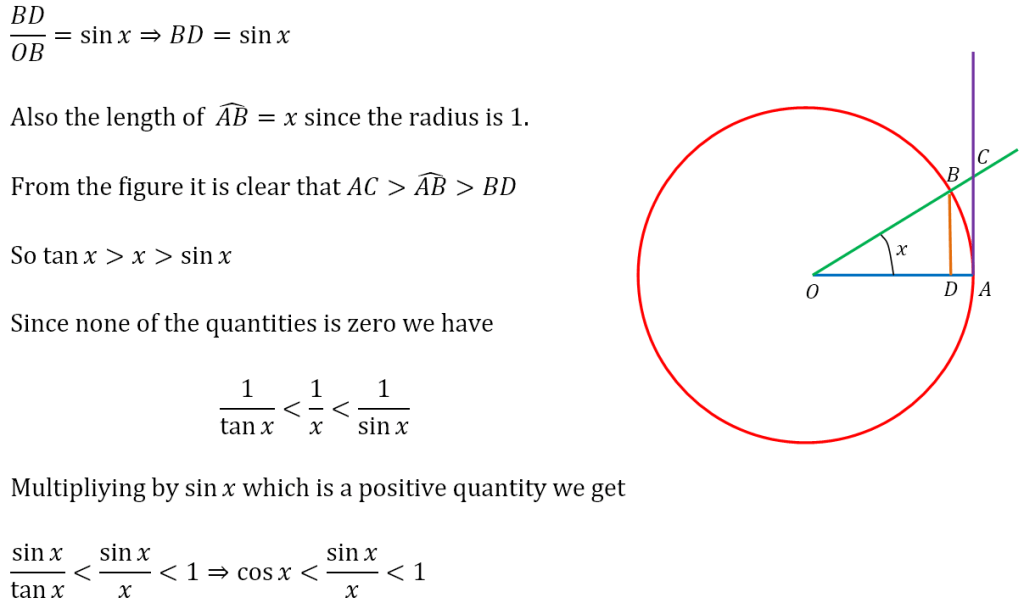
The Sandwich Theorem

Here we need to invoke a theorem known as the Sandwich theorem. Here it is

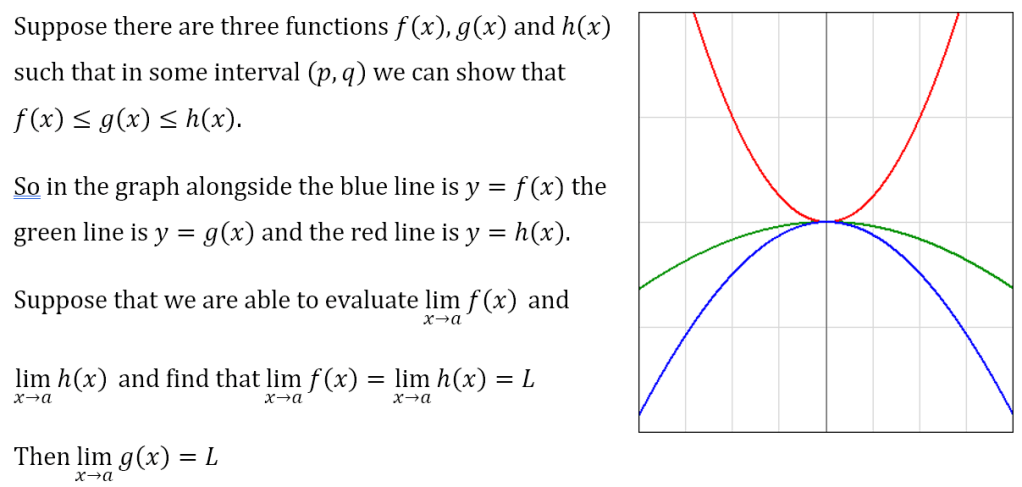
Let us return to our derivation of the limit and use the Sandwich theorem.

We now have enough under our belts to obtain the derivative of sin x. Let’s proceed.

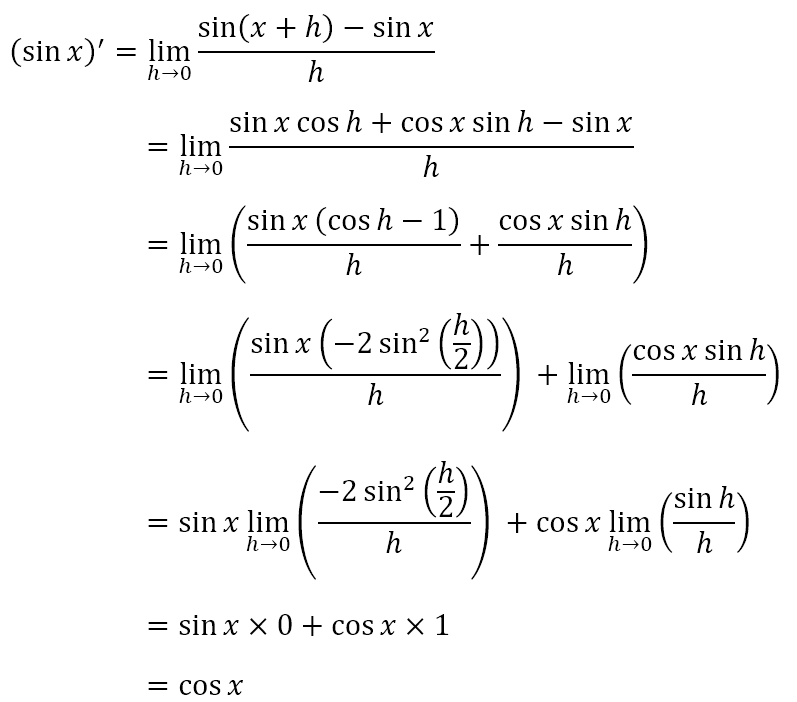
In a similar way we can show that (cos x)’ = -sin x.

Next Steps

In the derivations above, I have not shown all the ‘steps’ but have skipped some that are, in my view, decipherable by students who are willing to put in some additional effort. If any of the steps above is unclear, please do reach out to me. At the same time, I realize that, while the above results are old hat for students who have studied calculus, in many cases, these students have not been shown how the results are obtained. Shockingly, I have had students come to me in the twelfth grade having been introduced to differentiation but having no idea how the results are obtained. Due to this, I think this post is already quite heavy. So I will draw it to a close. In the next post, we will consider the derivatives of the exponential and logarithmic functions. Till then, be responsible and don’t drink and derive!