The Tripartite Fugue

Milestones on the Journey

After a three week break, most of which was spent grading IB papers, I am back. We continue with our series on complex numbers. By the time we last dealt with this, in Deriving Derivatives – Part 2, we had obtained the derivatives for a few functions as follows:

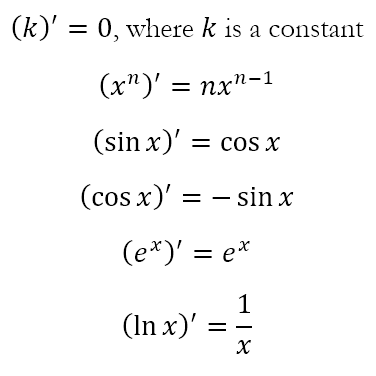
In the post that preceded it, that is Deriving Derivatives – Part 1, we also were able to obtain the following results:

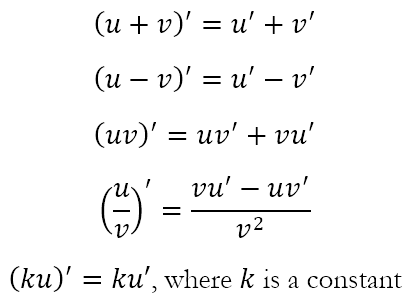
Of course, in Anticipating the Exponential Whirligig, we revisited a crucial result we had obtained during our series on e, namely that

During the series on e, the post Infinitely Expressed introduced us to the idea of infinite series. We explored the idea of infinite series in the post Serially Expressed, during which we derived the above result for the derivative of e^x. Let us now proceed with using what we know so far about infinite series to obtain similar expressions for sin x and cos x.

Infinite Series for sin x and cos x

We begin by assuming that

We also assume for now that this series converges. Now, we can differentiate the above equation repeatedly to obtain

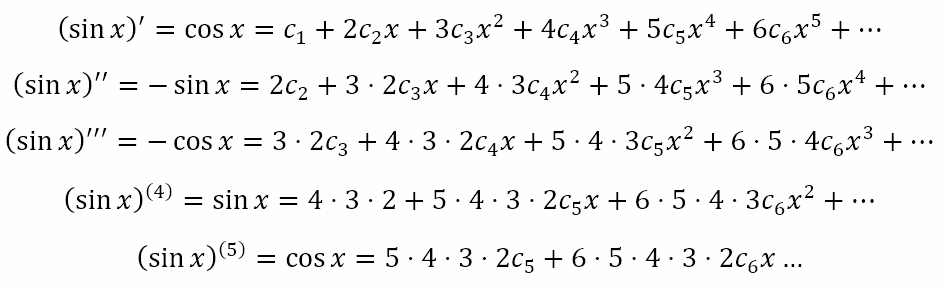
Note that, in the last two equations above, the superscripted (4) and (5), with the numerals 4 and 5 inside parentheses, indicates the 4^th and 5^th derivatives of the function respectively, in this case, sin x.

Now, we can substitute x = 0 in all the equations for sinx and its derivatives to obtain the following:

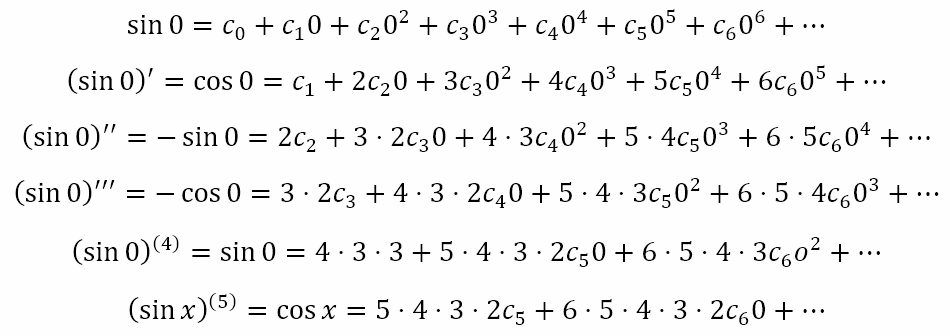
Now, we know that sin 0 = 0 and cos 0 = 1. This means that the above set of equations reduces to

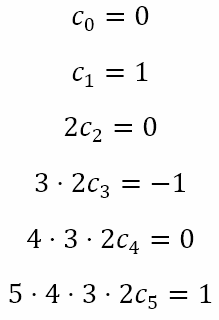
Now, we know that

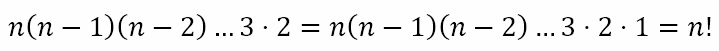
This means that the above set of equations can be written as

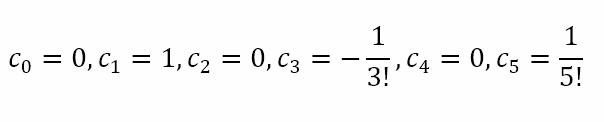
We can see that the constants with even subscripts are all zero. The constants with odd subscripts are the reciprocals of the factorial of the subscript with alternating positive and negative signs. Substituting this in the infinite series expression for sin x we get

In a similar way we can obtain

Assembling the Fugue

So, as of now, we have the following three infinite series

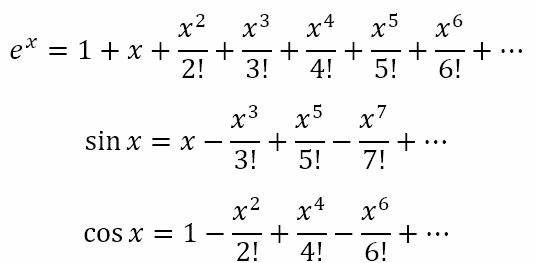
What we can observe from the above is that the series for e^x has terms with every power of x and all the coefficients are positive. The series for sin x has terms with odd powers of x and the coefficients alternate between positive and negative. Likewise, the series for cos x has terms with even powers of x and the coefficients alternate between positive and negative.

Now, recall that

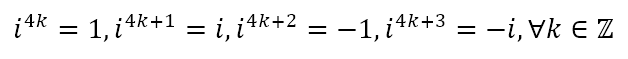
Now, in the series expression for e^x let us replace x with iθ. This will give us

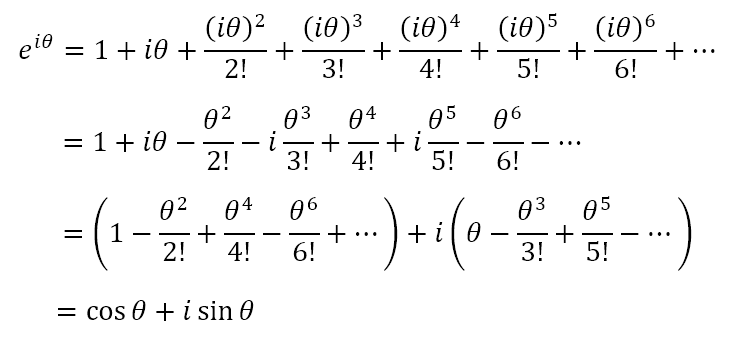
This is the exponential form of complex numbers that we have been pursuing for many weeks now. It links the exponential function to the sine and cosine functions. We can easily see that the modulus of this complex number is 1 while its argument is θ. In case you have forgotten what the modulus and argument of a complex number are, we had introduced the former in Modulating an Invariant Metric and the latter in Pole Vaunting.

Hence, a complex number z = x + iy can be written in polar and exponential form as follows:

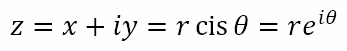
where

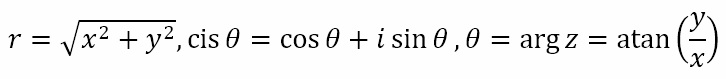
Here, r is the modulus of z and θ is the argument. Of course, care must be taken when determining the argument of z. When y/x is positive, it could be because both are positive, in which case the angle is in the first quadrant and atan(y/x) will give the correct value. On the other hand, both could be negative, in which case the angle is in the third quadrant, meaning that π radians or 180° need to be added to or subtracted from atan(y/x). In much the same way, when y/x is negative, it could be because x is positive and y negative, in which case the angle is in the fourth quadrant and atan(y/x) will give the correct value. However, it could be because x is negative and y positive, in which case the angle is in the second quadrant, meaning that π radians or 180° need to be added to or subtracted from atan(y/x).

The Journey Ahead

Now, the exponential form of complex numbers is a powerful form. However, me simply claiming this is so cannot suffice. So, in the next post, which will be the final one in this series, I will consider the exponential form in greater detail. We will also consider how it showcases the idea of rotation, linking it to the idea of negation that we first saw in A New Kind of Number.