Contacting Elliptical Polarity

Brief Recapitulation

In this post we continue with the series on conic sections. In the previous post, A Mathematical Shortfall, we introduced the ellipse and derived the equation of the ellipse in standard form. We also obtained the equation for the auxiliary circle of the ellipse and the equation of the tangent at a point on the ellipse and the condition for tangency in terms of the gradient (m) of the tangent. In this post, we will explore the chord of contact and the polar with respect to the ellipse.

Chord of Contact

Consider the ellipse

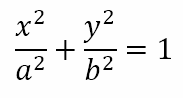
Recall that the equation of the tangent at the point (x₁, y₁) is

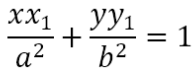
Let P(x₁, y₁) be a point outside the ellipse

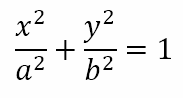
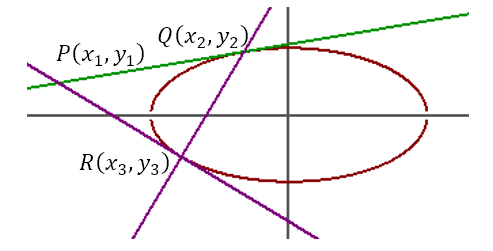
From point P tangents are drawn to touch the ellipse at Q(x₂, y₂) and R(x₃, y₃). This is shown in the figure below.

Since PQ is the tangent at Q, its equation must be

Since P lies on this tangent, its coordinates must satisfy the above equation. Hence,

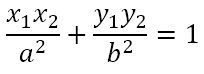
Since PR is the tangent at R, its equation must be

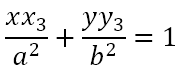
Since P lies on this tangent, its coordinates must satisfy the above equation. Hence,

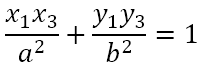
It follows then that Q(x₂, y₂) and R(x₃, y₃) satisfy the equation

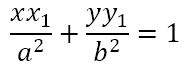
Since two points determine a straight line, this must be the equation of the chord of contact QR.

Pole and Polar

Having derived the equation of the chord of contact, let us proceed to derive the equation of the polar of a point with respect to the ellipse. Let P(x₁, y₁) be a fixed point placed anywhere relative to the ellipse. A line through P is free to pivot about P. In general, this line will cut the ellipse at two points. Suppose these points are Q(x₂, y₂) and R(x₃, y₃). Tangents are drawn to the ellipse at the points Q and R. Let these tangents intersect at S(h, k). This is shown in the figure below.

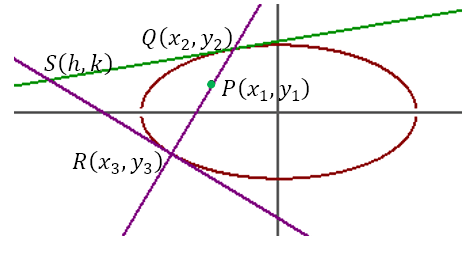
As the line through P pivots about P, the points of intersection of the line with the ellipse will change. Hence, Q and R will move. This means that the tangents at Q and R will move. Hence, the point of intersection, S, of the two tangents will move. Then the locus of S is known as the polar of P wrt the ellipse and P is known as the pole of the polar with respect to the ellipse. It can be seen from the diagram that QR is the chord of contact of S wrt the ellipse. Hence, its equation should be

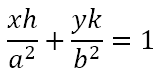
However, P lies on QR. Hence, its coordinates should satisfy the above equation. This gives us

Generalizing, we obtain the locus of S to be

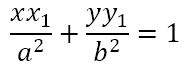
As just obtained, the polar of the point P(x₁, y₁) is

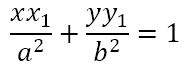
The point P(x₁, y₁) may be anywhere in relation to the ellipse for a polar to exist. If the point P lies outside the ellipse, the portion of it that lies inside the ellipse is the chord of contact while the portion that lies outside the ellipse represents the set of points actually reached by the polar. If the point P lies inside the ellipse, the entire line represents the set of points actually reached by the polar for then there would be no chord of contact.

If you wish to see how the chord of contact, pole and polar relate to an ellipse, you can click here for a Geogebra App that I created. With the checkbox on the top left unchecked, you can see how the chord of contact varies. Just click on the point P and drag it around! If you check the checkbox on the top left, you can explore how the pole and polar vary. Again, just click on the point P and drag it around to position the pole. I have made the line rotate automatically. This changes the positions of Q and R automatically and, therefore, the bright pink tangents at those two points. The point of intersection of these two tangents will move, tracing the green line, which is the polar.

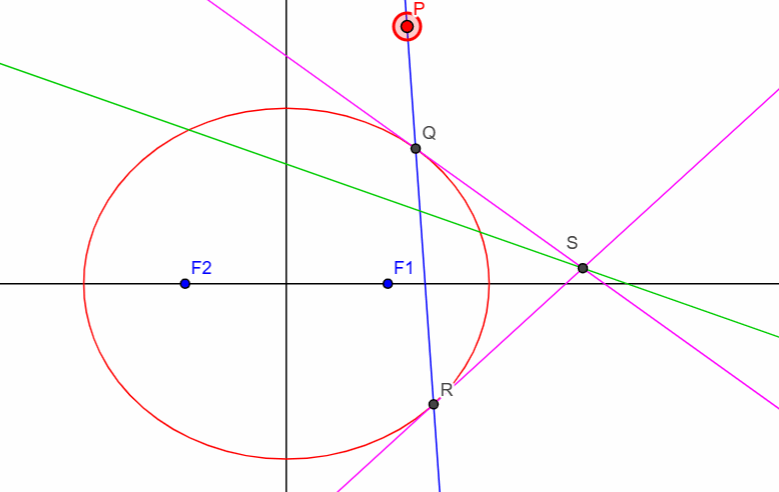
From the applet you will notice that the chord of contact technically only represents the part of the line that is inside the ellipse which the polar represents the part that is outside the ellipse. And when P is on the parabola, the chord of contact degenerates to the point P, meaning that the tangent itself is the polar. This is why all three features of the ellipse, as in the case of all the conic sections, share the same equation.

The Director Circle

The ellipse also has another interesting feature known as the director circle. It is the collection of all points from which tangents drawn to the ellipse are at right angles to each other. Recall the condition for tangency. Given the ellipse

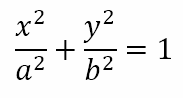
the line

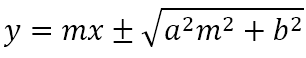
is always a tangent to the ellipse. Consider a point P(h, k). Let the tangent

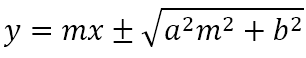
pass through P. Then the coordinates of P will satisfy the equation of the tangent.

This is a quadratic equation in m and if the tangents through P intersect at right angles then the product of the slopes of the tangents would be -1. From what we know concerning quadratic equations, this means that the constant term divided by the coefficient of x² must be -1. Hence,

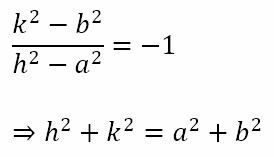
Generalizing we get the equation of the director circle is

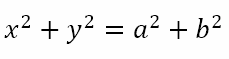
Hence, from any point on the above circle the two tangents drawn to the ellipse

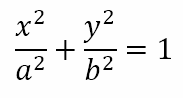
will be at right angles to each other.

The Ellipse and the Circle

If we compare the the ellipse and the circle we will see that setting b = a in all the equations related to the ellipse transforms the equations to those related to the circle. This is why the ellipse and the circle are related and the latter is said to be the degenerate form of the former. In particular, with respect to the previous figure, in a circle, the two foci, F₁ and F₂, are merged into the center of the circle. Hence, in a very real sense, the distance between the foci is a measure of the eccentricity of the ellipse. Recall that, when we derived the equation for the ellipse, we obtained the coordinates of the foci to be (ae, 0) and (-ae, 0). This means that the distance between the foci is 2ae, validating the intuition that the distance between the foci is linked to the eccentricity of the ellipse.

In these two posts we have briefly studied the ellipse. In the next two posts we will deal with the hyperbola, the last of the non-degenerate conic sections. Till then, I hope you have a week with no shortfalls.