Category: Complex numbers
-
Forms of Complex Numbers In the previous post, The Tripartite Fugue, we finally obtained the exponential form for complex numbers. As mentioned in the previous post, we will conclude our series on complex numbers today. Here I wish to explore a couple of aspects of complex numbers that become evident from the exponential form. I…
-

Milestones on the Journey After a three week break, most of which was spent grading IB papers, I am back. We continue with our series on complex numbers. By the time we last dealt with this, in Deriving Derivatives – Part 2, we had obtained the derivatives for a few functions as follows: In the post…
-
It has come to that time of the year when I grade the IB papers. This requires a significant amount of my time and also focus. So I will not be posting for the next few weeks. The next post will only be on 20 June 2025. In the meantime, you can check my series…
-
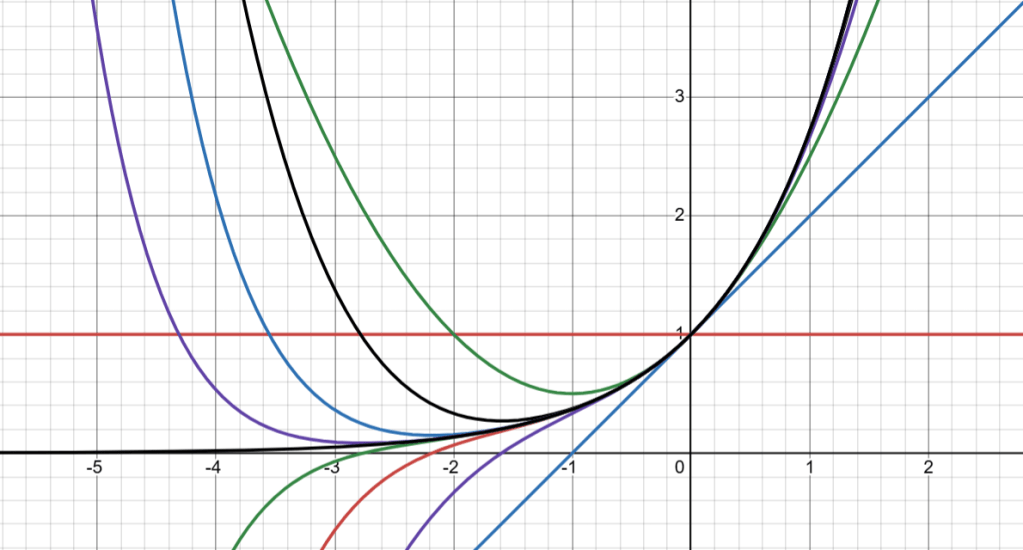
Revisiting Convergence We are in the middle of the second pit stop on our journey of exploring complex numbers. We have reached a point where I can introduce us to some infinite series, as mentioned in the previous post. Of course, we have encountered infinite series when we studied e as well as when we…
-

Signing In In the previous post, Deriving Derivatives – Part 1, which is part of the second pit stop in our exploration of complex numbers, we had derived the derivatives of xn and sin x. I had informed you that we will derive the derivatives of the exponential and logarithmic functions. In case some of you…
-

Rewinding a Bit We began our exploration of calculus last week with The Sky is the Limit. This is the second pit stop in our exploration of complex numbers. The first pit stop dealt with trigonometry. In the previous post we had looked at the idea of the limit, which I said was a central concept…
-
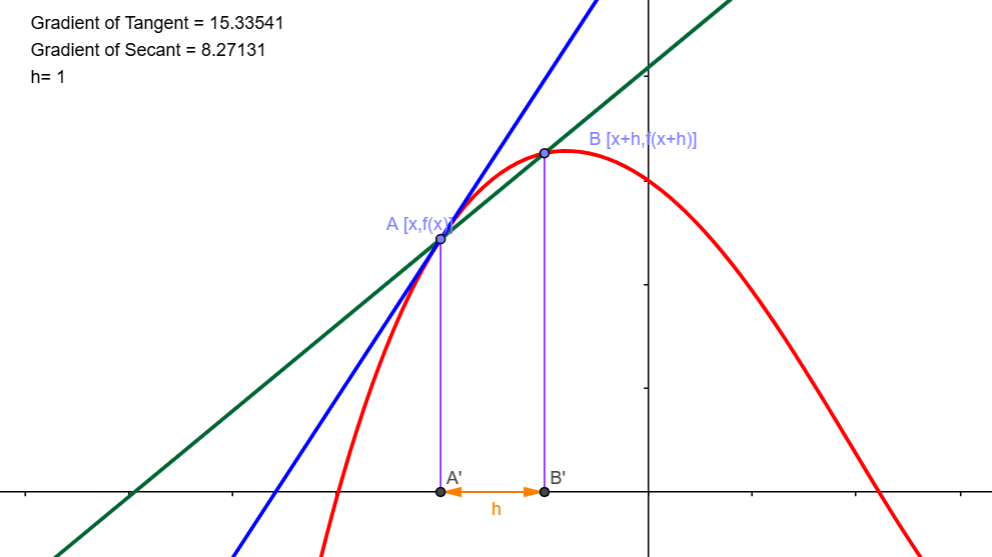
The Rationale We are in the middle of a series on complex numbers. In the previous post, Anticipating the Exponential Whirligig, we had come to a critical point, where I claimed that there was another way of representing complex numbers that is even more powerful than the polar form, which was itself more powerful than the…
-

Resumption Last week I had taken a break for Good Friday. For those who are interested, I used a random event for my sermon. If you’re interested, you can find it here. Anyway, with the break behind us, we resume the series on complex numbers. In the previous post of the series, Pole Vaunting, we…
-

Back on Track As we continue our series on complex numbers, we return to the main series of posts, having concluded what I called a ‘pit stop’ last week. The pit stop introduced us to trigonometry. It should be observed that I have only introduced trigonometric ideas that contribute to our understanding of complex numbers.…
-

Signaling the End In our study of complex numbers, we are reaching the end of a pit stop dealing with trigonometry. I ended the previous post by mentioning that the trigonometric functions are periodic in nature. I claimed that this is an important feature in the study of complex numbers. In this post, we will…
