
Recent posts
About
Category: Uncategorized
-
This will be the final post for 2025. And it is a short one. I will be taking a break of a few weeks after that and will resume on 16 January 2026. For this final post, I would like to consider another problem I recently came across, depicted in the figure below. Each of…
-
Problem 1: Pure geometry I recently came across two other interesting geometry problems, which I would like to tackle here. The first is depicted in the figure below. In the figure above, ΔABC is isosceles, with AB = AC and ∠A = 36°. Point X on side AB and point Y on side AC are…
-
Framing the Problem I recently came across an intriguing problem that I thought worth pursuing. It is represented by the figure below. We are given a triangle XYZ. On each of its sides, we construct a square so that the squares are outside the triangle. This gives us the squares XYCB, YZED, and ZXAF. Now,…
-
Presenting Problem I recently came across the following problem: Eight lamps, each with an on-off switch, are arranged in a circle. A lamplighter can flip (in other words, change the state of) the switches, but he is not allowed to flip just one at a time. When he switches lamps on or off, he is…
-
The Final Spur For some weeks now, we have been focusing on the conic sections. In the last post, A Mathematical Straight Couple, we introduced the pair of lines as a degenerate hyperbola. We saw that the joint equation of a pair of lines through the origin is This kind of equation, where the sum of…
-
Making the Case We are in the middle of a series of posts on conic sections. After the introductory post, Finding Refreshment in the Desert, I devoted three posts to the circle and two each to the parabola, ellipse, and hyperbola. In the previous post I had mentioned a degenerate conic section known as a pair…
-
Brief Recapitulation In this post we continue with the series on conic sections. In the previous post, A Mathematical Exaggeration, we introduced the hyperbola and derived the equation of the hyperbola in standard form. We also obtained the equations for the conjugate hyperbola, the auxiliary circle of the hyperbola and the equation of the tangent at…
-
The Riddle of the Name In this post we continue with our study of the conic sections. So far we have looked at the circle, the parabola, and the ellipse. Now we turn to the final non-degenerate conic section – the hyperbola. When we hear the word ‘hyperbola’, some of us may think of the…
-
The Riddle of the Name When I was in school, one of my English teachers (unfortunately I do not recall which one) taught us about the punctuation mark known as the ellipsis. An ellipsis is three dots (…) that indicate something is missing. It could a lack of words, such as…, well…, you see…, indicating…
-
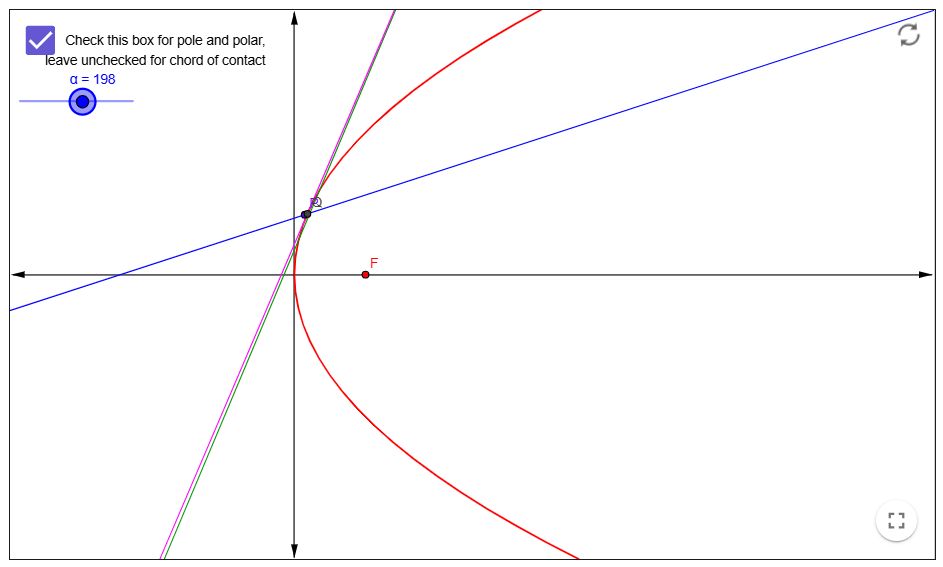
Brief Recapitulation In the previous post, titled Mathematical Parables, I introduced us to the parabola. Just to jog your memory, a conic section is a a geometric figure such that, for any point on the conic section, the ratio of its distance from a fixed point, called the focus, to its distance from a fixed…