My Unbounded Mathematical Trauma

The Initial Trauma

It was almost twenty years ago when I first heard the statement. It shocked me then. No, to be true to what I felt, it was as though someone had punched me in the gut. I felt a visceral response to the statement. And even today when I hear similar statements, it grinds my gears (😉 to those readers who understand the reference). It is the equivalent of hearing a mathematical heresy or numerical blasphemy. I kid you not! And I do not know what to say about the teachers who allow such heterodoxy (I use that word generously) into their classrooms.

On that fateful day, I was teaching trigonometry to the students. Of course, I do not know the exact problem we were tackling. Either my memory is not that sharp or I have suppressed some of it due to the trauma I experienced from the statement! What I do remember is that we were solving a trigonometric equation. As an example consider the equation below, which will represent the issue quite well:

tan θ = sin θ

One student suggested dividing the whole equation by sin θ to obtain:

1÷cos θ = 1

So I asked the class what would happen if sin θ = 0. They, like the good students they were, said that division by 0 is not permitted. I pressed my luck and asked them why it was so. No one could give me an answer. They had learned this from their teachers and had accepted it with a docility that I hope will not characterize any reader after reading this post!

So I asked them what 1÷0 is. And that’s when I heard it. On that fateful day, for the first time my still traumatized ears heard that 1÷0 equals infinity. Although I have heard this almost every year since I still shudder when I hear it.

In order that the reader would understand my trauma, I will first deal with why it is mathematically incorrect to say 1÷0 = ∞. Then we will address the issue of what 1÷0 would mean. Finally, we will se what would happen if, despite the meaninglessness of 1÷0, we allowed such division. Hold on to your hats!

No Place Called ‘Home’

During my reasonably long career as a teacher, I have had many students tell me that, especially in their physics classes and, to a lesser extent, their chemistry classes, they were told that, “One divided by zero equals infinity.” I have verified this independently with 3 physics teachers and 2 chemistry teachers. If the reader happens to be a physics or chemistry teacher who holds this position, I hope to convince you otherwise. You have been warned! If you happen to be a non-mathematics teacher who has realized and communicated to your students the falsity of the statement, then I thank you. However, if you happen to be a mathematics teacher who told your students that, “One divided by zero equals infinity,” I have to ask you, “Seriously?”

So why is it incorrect to say that 1÷0 = ∞? When comparing any two items it is crucial that we are comparing two things of the same kind. It is quite ridiculous to say, “An apple is less than a car.” Equally nonsensical is the statement, “A skirt is equal to a bolt.” And similarly meaningless is the declaration, “Tuesday is greater than May.” We can easily recognize that what makes these statements meaningless is the attempt to compare things belonging to different classes of objects – a fruit and a vehicle; an article of clothing and a fastener; a day of the week and a month.

So what do we have in the statement 1÷0 = ∞? On the left side of the equation we have two numbers and one mathematical operator. I have italicized the word ‘mathematical’ in the previous sentence because we have to ask ourselves what distinguishes ‘mathematical operators’ from ‘operators’ in general. A ‘mathematical operator’ is a function that takes some mathematical ‘entities’ as inputs and churns out a mathematical entity as its output. I will devote future posts to discussing the nature of some mathematical operators.

On the left we have the two numbers denoted by the numerals ‘1’ and ‘0’. Along with them is the division operator, denoted by the symbol ‘÷’. Now, the division operator takes two inputs, the first being the ‘dividend’ and the second the ‘divisor’. The output of the operator, that is, the result of the division, is the quotient. Now, the word ‘quotient’ is Latin for ‘how many times’. In other words, we are asking the question, “How many parts the size of the divisor can be accommodated in the dividend?” or “How many repetitions of the divisor will give us the dividend?” I will give only one example so as not to insult the reader’s intelligence. 15÷5=3 because the are 3 parts, each the size of 5, that give us 15.

But a ‘quotient’ must necessarily be a number since the question is ‘how many times?’ However, infinity is not a number! Here I must fault Wolfram Mathworld for its misleading statement, “Infinity, most often denoted as ∞, is an unbounded quantity that is greater than every real number,” and more ridiculously for its acceptance, even in an informal capacity, of the statement 1÷0 = ∞. We will address the ridiculousness of the statement shortly. But first let us address the important issue of language.

Of course, the word ‘quantity’ has been used by Wolfram Mathworld in an imprecise way. ‘Quantity’ refers to ‘how much’, for continuous entities, or ‘how many’, for discrete entities. Hence, 1 liter of petrol is ‘how much’ of petrol, since the quantify of petrol is a continuous entity, and ‘1 dozen eggs’ is ‘how many eggs’, since the quantity of eggs is a discrete entity. But the answer to ‘how much’ or ‘how many’ must be a number, even if denoted by a symbol (e.g. 2π as the answer to the question, “How many times does the radius of a circle fit into its circumference?”). The presence of ∞ on the right side of the equation means that infinity is a number. But if it is a number, what position does it occupy on the number line?

You see, the number line is a linear representation of all real numbers. If an entity is a real number, it must have a ‘home’ on the number line. But infinity famously does not have a ‘home’ on the number line because, if such a ‘home’ were found, the position just to the right of it would be a number greater than the number at this ‘home’, thereby contradicting the idea that infinity is greater than any real number. In other words, infinity is clearly not a number!

That makes the statement 1÷0 = ∞ meaningless since the left side, being the output of the division operator, must be a number, while the right side is not a number. Since it is ludicrous to equate a number to something that is not a number, the statement 1÷0 = ∞ is mathematically meaningless and should be removed from all mathematics resources as being untruthful and nonsensical. Of course, if we are comfortable with meaningless and nonsensical statements remaining in mathematics resources, we need to quit our jobs as mathematics teachers because we would have broken mathematics, as we will see shortly.

A Logistical Nightmare

But before we do that and to set the stage for it, let us consider what 1÷0 actually means. We saw that ’15÷5′ means, “How many parts of size ‘5’ can fit in ’15’?” It could also mean, “How many must be in each part of ’15’ if I want ‘5’ equally sized parts?” Hence, 1÷0 means, “How many parts of size ‘0’ can fit in ‘1’?” or “How many must be in each part of ‘1’ if I want ‘0’ equally sized parts?”

So, on the one hand, the equation 1÷0 = ∞ is mathematically meaningless because it equates the output of the division operator, which must necessarily be a number, to something that necessarily cannot be a number. On the other hand, even attempting to perform the division implied in the expression 1÷0 is meaningless because it describes an impossible distribution either of nothing or to no groups.

Now, mathematics has faced difficulties before, primarily with the issue of the closure property of the operations. I will devote a much longer post to this later. But let me briefly describe it here. Suppose we have the set of counting numbers (i.e. 1, 2, 3, etc.). If we take any two such counting numbers the sum will always be a counting number. For example, 23+73=96. It is impossible that the sum of two counting numbers is not a counting number. Hence, we say that the set of counting numbers is closed under the addition operator. The same can be said about multiplication. The product of two counting numbers will always be a counting number.

However, this is not true about subtraction. For example, 23-73 is not a counting number. Hence, we say that the set of counting numbers is not closed under the subtraction operator. However, so that we can still perform mathematics, we introduce the idea of zero and the negative counting numbers and call the new set of numbers the set of integers. And the set of integers is closed under addition, subtraction, and multiplication.

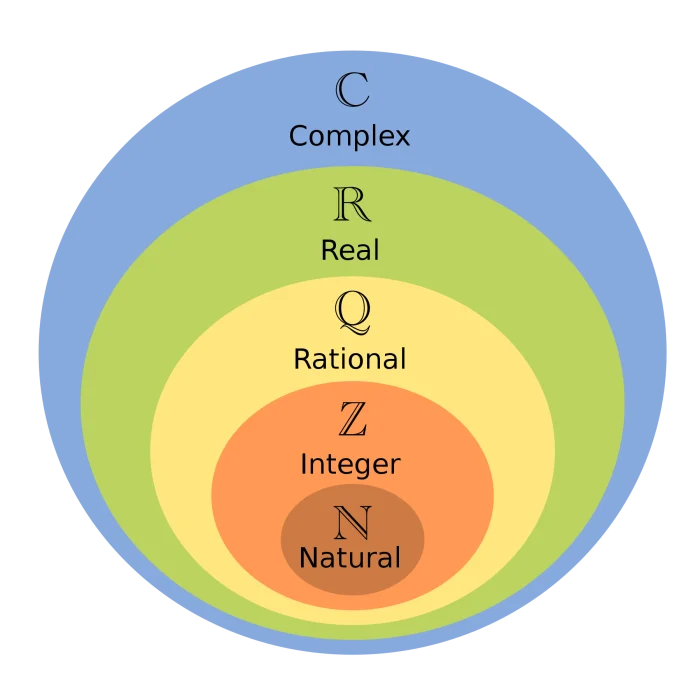
In similar ways we introduced rational numbers for closure under division and irrational numbers and later complex numbers for closure under exponentiation. If you do not understand this now, it’s ok. As promised, I will devote a future post to this. What you can gather, however, is that, whenever mathematicians were faced with some obstacle, they extended the set of numbers they were working with to overcome the obstacle.

Could it not be that we could define some new kind of number that will allow the expression 1÷0 to be meaningful? In other words, could the obstacle of the meaninglessness of 1÷0 be overcome by defining some new kind of number?

Some readers will already know that the answer to the previous question is, “No!” In fact, when I mentioned the rational numbers, those who remembered the definition would likely have been clued in to where I was going with this line of argumentation. Let me explain.

A rational number is defined as a number that can be expressed as p÷q, where both p and q are integers. However, there is one condition. The definition includes the condition q≠0, thereby prohibiting division by zero, the very conundrum with which we are wrestling! While we may be familiar with the definition, it does not tell us why it prohibits division by zero. Surely if mathematicians could have just defined some new kind of number to solve this ‘division by zero’ obstacle, they would have done just that. After all, they have had no qualms contriving new kinds of numbers to circumvent obstacles they faced in the past. Why then does that condition q≠0 persist? Is it not a clear indication that, in the face of the ‘division by zero’ obstacle, the mathematicians have just thrown up their hands and thrown in the towel, in reverse sequence, of course?

Mathematical Heresy

So what would happen if, despite the meaningless of the expression 1÷0, we permitted such mathematical heresy? Consider the following:

0=0

⇒0×1=0×2

There is nothing wrong with this equation since both sides evaluate to 0. However, dividing this equation by 0 (since we are now allowing it), we get

⇒1=2

Something has definitely gone wrong since we now have a statement that is clearly incorrect. In other words, by allowing division by zero we have proved an incorrect statement. And once we have proved one incorrect statement, we can prove any incorrect statement just by doing some creative but otherwise legitimate arithmetic manipulations. Want to prove a rational number is equal to an irrational number? Well, we can start by taking the square root of both sides to get:

1=2

⇒√1=√2

⇒1=√2

Here the left side is a rational number while the right side is irrational! Want to prove π=1? Here it is:

1=2

⇒1-1=2-1

⇒0=1

⇒0×(π-1)=1×(π-1)

⇒0=π-1

⇒π=1

All of mathematics is broken now because we can prove anything under the mathematical sun! And all this because we allowed division by zero.

Now, when mathematicians were faced with the prospect of taking the square root of negative numbers, they became creative and extended the number system to the set of complex numbers. Even though we are told from very early in our schooling that the product of two positive numbers is a positive number and the product of two negative numbers is a positive number, we are later introduced to a kind of number which when multiplied by a similar kind of number gives a negative product. Even though initially mathematicians were reluctant to include the imaginary numbers as legitimate numbers, they finally overcame their reservations. Today, hopefully no mathematics student from Grade 12 onward would bat an eyelid at the inclusion of these numbers.

What, then, about division by zero has proven to be so intransigent that mathematicians have thrown in the towel and thrown up their hands, now in this order itself, in defeat? With the issue of finding square roots of negative numbers, mathematicians had the option of saying, “There are no real solutions,” or something of the kind. They had the option of saying that the set of real numbers was not closed under exponentiation, thereby allowing them the possibility of later thinking of a new kind of number that would allow the new set of numbers to be closed even for exponentiation.

A Small Sacrifice

However, division by zero is a problem of a different kind. It ruins the whole system, which is why I have called it ‘mathematical heresy’. It is one single, simple idea, which, if permitted to enter the sphere of mathematics, would spell the end of mathematics. It is a kind of rabid animal that bites the hand that feeds it. It is a parasite that sucks the life out of the host. It is a cancer that quickly metastasizes and consumes the whole body.

Hence, in order to have a working body of mathematics in which contradictory statements cannot be proven true, mathematicians have chosen to make a small sacrifice. To this wonderfully liberating and free discipline, they had added one small limitation and constraint. They have chosen to make a small sacrifice so that not just mathematicians but the whole world can benefit from the beauty and elegance, simplicity and power of mathematics.