Serially Expressed

Revisiting Convergence

We are in the middle of the second pit stop on our journey of exploring complex numbers. We have reached a point where I can introduce us to some infinite series, as mentioned in the previous post. Of course, we have encountered infinite series when we studied e as well as when we studied π. An infinite series is simply the summation of all the terms of an infinite sequence.

In case the preceding sentence was confusing, let us recap a bit. A sequence is a succession of numbers generated according to a well defined rule. A sequence can have a finite number of terms or it could be an infinite sequence. A series is formed by adding the terms of a sequence. An infinite series can converge, diverge, or oscillate. A classic case of such a series is the geometric series. We considered the geometric series in Naturally Bounded?, the second post in the series on e. There, I only considered a single case where the common ratio r was 1/2. That series converged. In general, a geometric series will converge if the common ratio lies between -1 and +1. In all other cases, it will diverge. And if r is negative, the series will also oscillate, converging while oscillating if r is between -1 and 0 and diverging while oscillating if r is less than or equal to -1.

Conditions for Convergence

What this means is that, when we are faced with an infinite series, there will be conditions under which the series will converge. When these conditions are not met, the series will diverge, either oscillating or not oscillating.

So suppose we have an infinite series

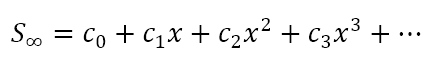
We can define the partial sum of n +1 terms as

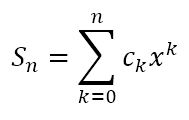
Now, if

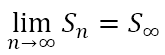
we can say that the series converges and that it converges to the finite sum of S_∞. In general, a necessary but not sufficient condition for a series to converge is that each term approaches zero. That is,

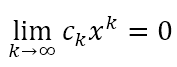
However, this test is not sufficient to guarantee that the series converges. For that, we have to apply many other tests. However, this is not what I wish to focus on. For now, let us simply assume that the series we will introduce are convergent. Will will then be able to obtain some rather intriguing results.

Infinite Series for e^x

So, suppose that

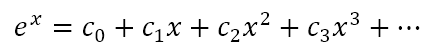
is a convergent series. Now, from the previous post we know that the derivative of e^x is e^x. From the post that preceded it, we know that the derivative of xⁿ is nx^{n – 1}. So, if we differentiate the above equation, we will get

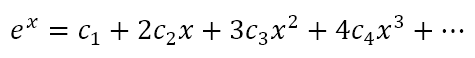
We can differentiate this again to get

We can continue in this manner ad infinitum. However, let us see what the value of all of these are when x = 0. When x = 0, e^x = e⁰ = 1. Also, all terms with x^k will become 0, leaving us with

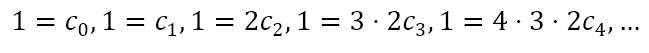
Rearranging each equation, we get

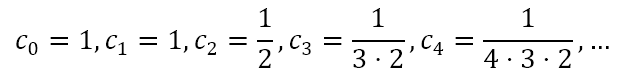
Recognizing that n! = n(n – 1)(n – 2)···3·2·1, and defining 0! = 1, we can write the above as

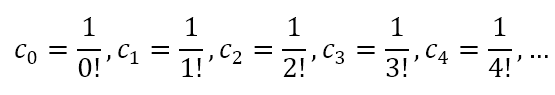
From this we can write the infinite series for e^x as

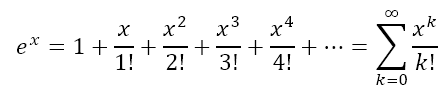
In the post Infinitely Expressed we looked at the speed with which a series converged. How does this series compare? The table below gives us the relevant information

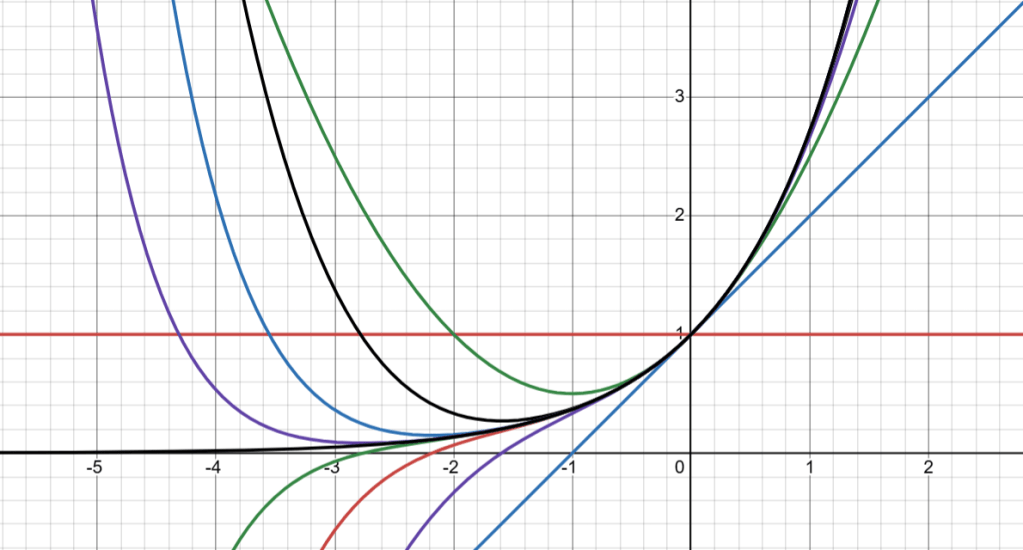
What we can see is that, as n increases, the error decreases by about one order of magnitude for each increased value of n. In the aforementioned post, we had seen that this series does not converge very quickly and we introduced other series that converge much more rapidly. However, here we are not concerned with the speed with which the series converges. Rather, the simplicity of the terms themselves provide a strange allure. From the image at the start of this post we can see how each additional term makes the resulting series more closely approximate the graph of y = e^x.

Infinite Series for sinx

Suppose now we attempt to obtain a similar infinite series for sinx. So let us consider that

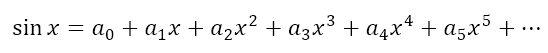
When we repeatedly differentiate the equation we will obtain the following

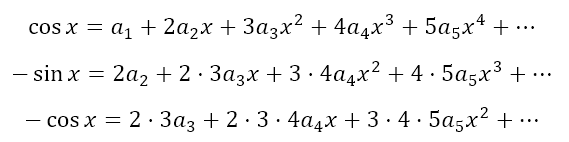
Now, if we put x = 0, we will have sinx = 0 and cosx = 1. Then we will obtain

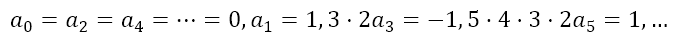
Rearranging these equations we get

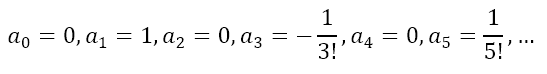
From this we can obtain

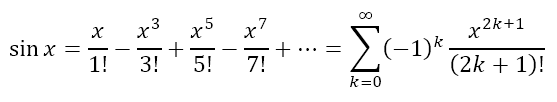
Infinite Series for cosx

In a similar way, for the cosx function, we can obtain

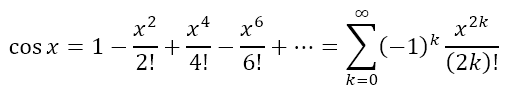
Setting the Stage

So far we have obtained infinite series expressions for e^x, sinx, and cosx. This gets us to the point where we can use these series to obtain the exponential form of the complex numbers. We will deal with that in the next post. Hence, this pit stop too has come to an end. We have, quite obviously, only dealt with those concepts in calculus that directly play a role in determining the exponential form of the complex numbers. Once I have concluded with the series of posts on complex numbers, we will revisit calculus. But till then I hope that this short pit stop has been helpful in your reaching the realization that calculus is not something to fear.