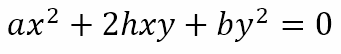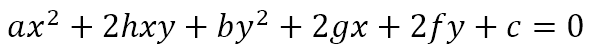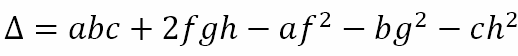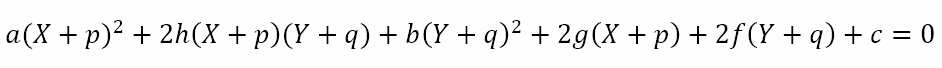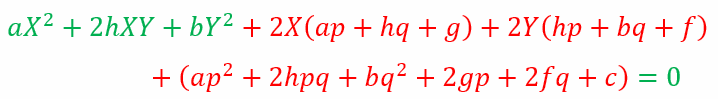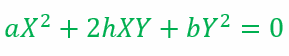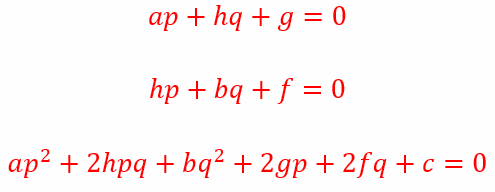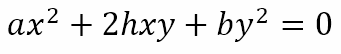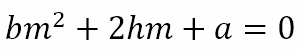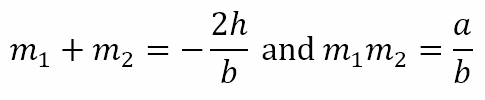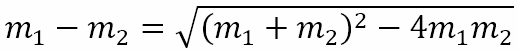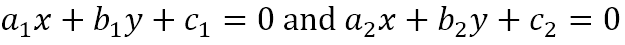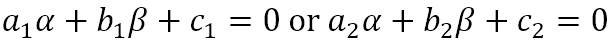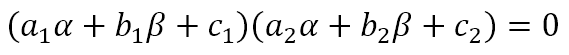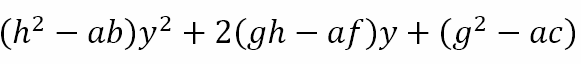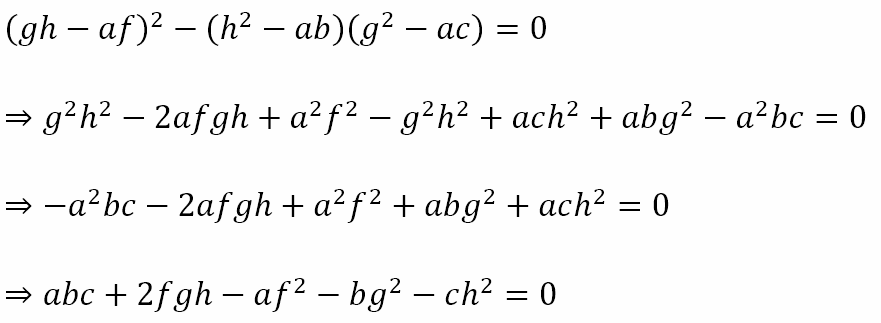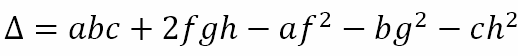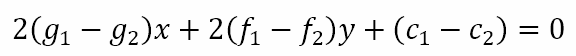Recent posts

About

A non-violent anarchist Mathematics teacher and Christian who has views about everything under the sun.

  • The World of Sagacious Selections

    Recapitulation

    (Source: i-Scoop)

    In this post we continue with the series on Counting Principles. Whereas we devoted the previous post to permutations of special kinds, we will turn our attention today to the matter of combinations. In Arranging and Choosing we saw that the binomial coefficients are related to the elements of Pascal’s triangle. We saw that the process of expanding an expression like (a + b)n involves multiplying a + b by itself n times. This involves choosing either a or b from each factor. We were, therefore, able to show that the (r + 1)th element of the nth row of Pascal’s triangle is the sum of the rth element of the (n – 1)th row and the (r + 1)th element of the (n – 1)th row. In symbolic notation,

    While we proved this result with algebra, I claimed that the algebraic method, involving pure brute force of algebraic manipulation, did not yield any particular insight. However, we proved the above result using

    and arguing from how a particular element on the left side is obtained by adding two terms on the right side. This sort of argumentation does not use algebra. However, the argument in Arranging and Choosing is not technically what is called a ‘combinatorial argument’. So, what is a combinatorial argument? Let us learn with a few examples.

    Combinatorial Arguments

    Example 1

    We begin with the same result we proved earlier. Suppose we have n distinct items and we wish to choose r out of them. This can obviously be done in nCr ways. Now, let us focus on one particular item (say A) out of the n items. The group of r items that are selected either contains A or does not contain A. If the selection contains A, then we have to choose r – 1 more items from the remaining n – 1 items, which can be done in n – 1Cr – 1 ways. If the selection does not contain A, then we still have to choose r items from the remaining n – 1 items, which can be done in n – 1Cr ways. Since the selections that contain A and do not contain A are mutually exclusive (meaning they have no common members) and exhaustive (meaning that there are no other possibilities), it follows that

    As an example, suppose we have to choose 6 items out of 20. This can be done in 20C6 = 38,760 ways. Now, if one of the items is A, then the selection either contains A or does not contain A. If it contains A, then we have to select 5 more items from the remaining 19 items, which can be done in 19C5 = 11,628 ways. If it does not contain A, then we have to select 6 items from the remaining 19 items, which can be done in 19C6 = 27,132 ways. It is easy to check that 11,628 + 27,132 = 38,760. This is an example of the addition principle that we dealt with in Down for the Count.

    Example 2

    Let us consider another result, namely

    We proceed as follows. Suppose we have n items and we have to select r of them for some purpose. This obviously can be done in nCr ways. However, by selecting the r items for the purpose, we automatically create a selection of the remaining n – r items not for that purpose – that is for some other purpose. Selecting n – r items for some other purpose can obviously be done in nCn – r ways. Since the selection of r items automatically creates a selection of the remaining n – r items, the number of ways must be equal. Hence, nCr = nCn – r .

    Example 3

    Now let us try to prove

    We proceed as follows. Suppose we have n items from which we have to select r items. This can be done in nCr ways. Now suppose we select k items from the r. This can be done in rCk ways. The two selections can obviously be done in nCr rCk ways. But we can make these selections in a different way. Let us first select the k items from the original n items. This can be done in nCk ways. Now we have to select r – k items from the remaining n – k items, which can be done in n – kCr – k ways. The two selections can obviously be done in nCk n – kCr – k ways. Since in both cases we end up with r – k items for one purpose and k items for a second purpose, the number of ways must be the same. Hence, nCr rCk = nCk n – kCr – k.

    An example of this last result is as follows. Suppose we have a class of 30 students. We need to select a committee of 7 members within which we select a sub-committee of 3 members. Then we can first select the entire committee, which can be done in 30C7 = 2,035,800 ways. Then we select the sub-committee, which can be done in 7C3 = 35 ways. This gives a total of 2,035,800 × 35 = 71,253,000 ways. Alternately, we select the sub-committee first, which can be done in 30C3 = 4,060 ways. Now we have to choose the remaining 4 members of the committee from the remaining 27 students, which can be done in 27C4 = 17,550 ways. This gives a total of 4,060 × 17,550 = 71,253,000 ways. This is an example of the multiplication principle that we dealt with in Down for the Count.

    Binomial Identities

    Having considered some combinatorial arguments, we turn our attention to the binomial coefficients themselves. Since there is a pattern leading from one row to the next, there must be some relationships that hold among these coefficients. For simplicity in proposing and proving these relationships, let us take a = 1 and b = x in the expansion of (a + b)n, which becomes (1 + x)n.

    Example 1

    Using the normal binomial expansion we obtain

    If we substitute x = 1 in the above we get

    We can verify this by considering a few rows of Pascal’s triangle. For example

    We can see that the identity holds true for the first 5 values of n.

    Example 2

    Now, if we substitute x = -1 in the expansion of (1 + x)n, we will get

    We can verify this for the first few rows of Pascal’s triangle. For example

    Again, we can see that the identity holds true for the first 5 values of n.

    Example 3

    We can even use differentiation to obtain various results. For example, consider the expansion

    If we differentiate both sides with respect to x we will get

    Now, if we substitute x = 1 in the above equation, we will get

    Again, we can verify this for the first few rows of Pascal’s triangle. For example

    Once again, we have seen that the derived identity holds for the first 5 values of n.

    Example 4

    We can carry the idea of differentiation further as follows. We know that

    If we multiply both sides by x we will get

    Now, if we differentiate with respect to x we will get

    Once again, we can verify this for the first few rows of Pascal’s triangle. For example

    So, we have verified the result for the first 3 rows of Pascal’s triangle.

    Parting Shot

    What we have seen in this post is that we can use logical arguments to obtain relationships between binomial coefficients. We can also use simple algebra and calculus to obtain other relationships. As seen in the last example, we can multiple (1 + x)n by other terms to obtain further identities. The results are quite obviously endless. For example, I leave the reader to attempt to prove that

    Perhaps a hint would help. Consider the expansion of

    If you wish to check the proof, click here.

    Our study of counting principles is not over, though. There is much more left to go. In the next post, we will consider how to obtain the number of divisors and sum of the divisors of any natural number without actually listing the divisors or counting them. And we will consider the technique of partitions. Till then, the ball is in your court.

  • A Penchant for Permutations

    Refresher

    Two weeks back, we started a new series on Counting Principles. In Down for the Count we looked the the basic multiplication and addition principles of counting. In Arranging and Choosing we introduced the ideas of permutations and combinations. In this post, we will consider circular permutations and permutations with restrictions.

    Circular Permutations

    When we introduced permutations, even though we did not mention it explicitly, the implicit understanding was that we were arranging the objects in a row. In fact, this is not necessarily the case. However, if we are able to call one position the ‘first’ position and another the ‘second’, etc., then what we have, in effect, is a row of positions since we can place the positions in a row according to their ‘number’.

    The knights of the round table. (Source: World History)

    Now, if we arrange the positions in a circle, what we lose is the ability to name a position as genuinely ‘first’. As the legendary round table of Arthur asserted, there is no ‘first’ in such a seating arrangement. Since there is no head, there is no primacy given to any particular position. We are only left with the relative positions and can say, “Person A is seated to the right of person B” or “Person B is seated to the left of person A.”

    Now suppose there are 5 distinct objects that need to be permuted and placed in a circle. Two of the permutations are ABCDE and BCDEA. These are shown below

    Since no position is a ‘starting’ positions or ‘first’ position, the two linear permutations above represent the same circular permutation, with A→B→C→D→E→A, being the progression if we went clockwise around the circle. We can easily see that the permutations CDEAB, DEABC, and EABCD represent the same circular permutation. Hence, there are 5 linear permutations that represent the same circular permutation. This simply represents having 5 options for the top position.

    If we generalize this to n objects, we can see that we will have n linear permutations that represent the same circular permutation. Now, n objects can be permuted in n! ways, as we saw in the previous post. This means that n objects can be permuted in a circle in

    We can extend this further to permuting r out of n objects. We know that r out of n objects can be permuted in nPr ways. However, for each set of r objects, there will be r linear permutations that represent the same circular permutation. This means that r out of n objects can be permuted in

    Permutations of Non-Distinct Objects

    Now suppose we do not have distinct objects. Rather, there are some objects that are identical. Let us consider a small set to get started. Now, instead of 5 distinct objects, let us consider 5 objects, 2 of which are identical. Hence, we could consider the set to be A, A, B, C, D. Note that the two ‘A’s are identical. Hence, it is impossible to distinguish between them. However, for the sake of this illustration, let us use subscripts to indicate patterns. So the two ‘A’s are A1 and A2.

    Now, it is clear that the patterns A1A2BCD and A2A1BCD will be indistinguishable since both will appear as AABCD. In other words, there are 2 patterns that are indistinguishable from each other. In a similar way, BA1CA2D and BA2CA1D will appear as BACAD. What this means is that, no matter where we place the two ‘A’s, there will be two permutations that will be indistinguishable from each other.

    What happens if there are 3 identical objects (e.g. AAABC)? Well, we can see that the patterns A1A2A3BC, A1A3A2BC, A2A1A3BC, A2A3A1BC, A3A1A2BC, and A3A2A1BC will all appear as AAABC. Hence, there are 6 permutations that will be indistinguishable.

    We can see that, if there are p objects that are identical, then there will be p! permutations that will be indistinguishable, all of which represent permutations in which the identical objects occupy the same positions in the pattern. Hence, if there are n objects, p of which are identical, they can be permuted in

    We can extend this to multiple kinds of identical objects. Suppose we have n objects with p1 of one kind, p2 of a second kind, etc. up to pk of a kth kind. Then the number of permutations will be

    Let’s apply this. Let’s say I have 50 tiles, 4 of which are blue, 5 of which are red, and 10 of which are green, all others being distinct. Then then number of permutations will be

    That’s 2.91… septendecillion permutations! I bet you learned a new word here!

    Permutations with Restrictions

    We can also consider a different kind of permutation in which we have some restrictions. For example, suppose we have 5 distinct objects (e.g. A, B, C, D, and E), which have to be arranged such that two of them, say A and B, have to be adjacent to each other. To find the number of permutations, we consider the group formed by A and B to be a distinct group, say X. Then, we have 4 distinct objects, C, D, E and X, which need to be permuted. This can obviously be done in 4! = 24 ways. However, the objects A and B can be permuted among themselves in 2! = 2 ways. For example, the permutation CXDE can be CABDE or CBADE. Hence, the total number of permutations is 4! × 2! = 24 × 2 = 48.

    We can generalize this. Suppose we have n distinct objects, p of which need to be placed in a group and arranged among themselves. Hence, there are n – p distinct objects which have no restrictions. Then the number of distinct objects will be n – p + 1, including the group with p objects, which can be permuted in (n – p +1)! ways. However, the p objects can be permuted among themselves in p! ways. Hence, the total number of permutations will be (n – p + 1)! × p!.

    Let’s consider an example. Suppose there is a group of 20 people, 5 of whom must be seated together. Then then number of permutations will be

    Of course, we can extend this further. Suppose there are n distinct objects that need to be arranged such that a group of p1 objects need to be together, another group of p2 objects need to be together, and so on till a group of pk objects need to be together. Note that each group will count as 1 object. Hence, the effective number of objects, including distinct objects and groups, which need to be permuted will be

    Hence, the number of permutations, including the permutations within the groups, will be

    Let’s try this out. Suppose there are 50 seats in a bus and 50 passengers. Among the passengers are a family of 5, a couple, and a group of 11 friends. If the groups have to sit together, the number of permutations will be

    That’s 98.99… quindecillion permutations!

    Looking Ahead

    In this post we have looked art some different kinds of permutations, where the objects are arranged in a circle or where some of the objects are identical or where some distinct objects need to be kept together. Of course, there are cases where we may need to ensure some objects are not placed together, as in the case of rivals or bitter enemies. This is a much more complex situation than simply keeping a group together. So we will look into that in a post much later. However, in the next post, we will turn our attention to combinations and look at what are known as combinatorial arguments, which will help us to derive identities using the binomial coefficients solely through logical argumentation rather than through algebraic manipulation. Auf wiedersehen!

  • Arranging and Choosing

    Defining Terms

    (Source: Willing Ways)

    In the previous post, Down for the Count, we started a series on counting principles. We looked at the multiplication and addition principles of counting and I promised that, in this post, we would look at permutations and combinations, as well as the relationship between combinations and the binomial coefficients. So, what do these strange words mean?

    A permutation is an arrangement. Hence, if I have three objects, A, B, and C, I could arrange them as ABC, ACB, BAC, BCA, CAB, and CBA. Each of these, while containing each of the objects, represents a different ordering of the object and, hence, a different permutation. Now, suppose I have to choose two out of the three objects. I could choose A followed by B or B followed by A. But in both cases I have chosen A and B. What is end up with, in other words, does not depend, in this case, on the order in which I chose the objects. Both of them represent the same combination of A and B. Hence, if the order is important, we call it a permutation. And if order is unimportant, we call it a combination.

    The term ‘binomial coefficient’ is a little more difficult to explain. Consider the expression a + b. Since there are two terms, a and b, this expression is called a binomial. Now, consider the expression (a + b)n. We know that this means the expression a + b is multiplied by itself n times. For example, (a + b)2 = a2 + 2ab + b2. The coefficients of the terms are 1, 2, and 1. Since these are obtained by expanding the power of the binomial, they are called ‘binomial coefficients’. Similarly, the binomial coefficients of (a + b)3 are 1, 3, 3, and 1, while those of (a + b)4 are 1, 4, 6, 4, and 1.

    Enumerating Permutations

    Suppose I have two distinct objects, A and B. I need to place them in some order. I can choose either A or B to occupy the first position. Hence, for the first position, I have 2 options to choose from. Once I do this, I am left with the second object and am forced to place it in the second position. This means that I have 2 × 1 = 2 ways of arranging A and B, namely AB or BA.

    Now, if I have three objects A, B, and C, I have 3 options for the first position. Once I have placed that object, I am left with 2 objects, which can be arranged, as we have seen in the previous paragraph, in 2 ways. Since I have to arrange all three objects, I use the multiplication principle and conclude that there are 3 × (2 × 1) = 6 ways of arranging A, B, and C. These have already been listed earlier.

    Now, if I have four objects A, B, C, and D, I have 4 options for the first position. Once I have placed that object, I am left with 3 objects, which can be arranged, as we have just seen, in 6 ways. Against, using the multiplication principle, we can conclude that there are 4 × (3 × 2 × 1) = 24 ways of arranging A, B, C, and D. These are ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB, and DCBA.

    We can see that, if we proceed this way, the number of ways of arranging 5 objects would be 5 × 4 × 3 × 2 × 1 = 120 ways. We can generalize this and conclude that, given n distinct objects, the number of ways of permuting all of them would be

    Now, suppose we do not wish to arrange all the objects, but only r of the n available objects. We can obtain the following table.

    The first row in red contains the position numbers. The second row indicates the number of options available for that position. Note that the third row is simply the sum of the items in the preceding two rows, which all happen to be n + 1. It follows then that the number of ways of permuting r out of n items is

    This is a cumbersome formula. However, we can make it simpler as follows

    We can use this formula quite easily now. For example, if we wish to arrange 9 out of 15 distinct objects, then we number of permutations is

    The answer of 1,816,214,000 should also give a reason why, in many cases, we simply prefer to write it in short form as 15P9. The large numbers are due to the fact that the factorial (n!) grows at a remarkably fast pace. The table below gives a comparison of the growth of various common functions.

    As can be seen, after a relatively slow start, the factorial function just balloons up. It will eventually grow faster than any exponential function because, for any function y = ax, for values of n > a, the multipliers for n! will be greater than the multipliers for ax, which is a. As the table above shows, 25! > 1025. If we had 25 distinct objects and wish to arrange all of them, we would have 15 septillion, 511 sextillion, 210 quintillion, 43 quadrillion, 330, trillion, 985 billion, 984 million arrangements. Just to give you an idea of how large this number is, if you started at the big bang, forming one arrangement every 1 second for the 14 billion years of the life of the universe so far, you would need more than 35 million such universes before you were able to finish every arrangement!

    Enumerating Combinations

    Anyway, there are times when the order of objects does not matter. For example, if we are selecting a 3-member committee from person A, B, C, D, and E, it does not matter if we chose them in the order DBE or BED, etc. Only the final members selected would matter. Now, recall that permuting 3 out of 5 objects can be done in 5P3 ways. However, this represents all the permutations of the three objects selected. Hence, for the set {B, E, D} we have 3! ways of permuting them (i.e. BED, BDE, DBE, DEB, EBD, and EDB), all of which constitute the same selection of the set {B, E, D}. In other words, if we are only concerned about the objects selected and not the order in which they are selected, then 5P3 represents an ‘over counting’ by a factor of 3!. This means that the number of ways of selecting 3 objects from 5 objects would be

    We can extend this to a more general case. Given n distinct objects, we can arrange r of them in nPr ways. However, the r objects can be permuted among themselves in r! ways, all of which represent the same selection. Hence, nPr represents an ‘over counting’ by a factor of r!. This gives the number of ways of selecting r out of n distinct objects to be

    Now, we can see that, given n objects to choose from, we can choose anywhere from 0 of the objects to all of the objects. However, if we put r = 0 or r = n in the above formula, we get

    However, common sense tells us that there is only 1 way to choose none or all the n objects. Because of this 0! is defined to be equal to 1.

    Now, if we tabulated the values of nCr, we would get a table as follows.

    The Binomial Coefficients and Pascal’s Triangle

    We can also prepare the first 8 rows of Pascal’s triangle and obtain

    We can see that the values of nCr match the elements of the rth row of Pascal’s triangle. Why is this?

    Consider the expression (a + b)n. As mentioned earlier, when we expand this, we are multiplying a + b by itself n times. So we have

    where there are n sets of parentheses. Now, to complete the multiplication, we need to multiply each element from each set of parentheses by each element in every other set of parentheses. When we get to a particular binomial, we have to decide whether to choose a or to choose b. We cannot choose both, nor can we choose neither. In the end, we will multiply n elements, one from each set of parentheses. Hence, the power of every such product will be n, distributed between the power of a and the power of b. Hence, if the power of a is r, the power of b will be n – r, yielding terms that have arbn – r. However, this means that we have to choose r sets of parentheses to contribute the a, thereby making the other n – r sets of parentheses to contribute the b. Hence, we have to ask, “In how many ways can we choose r sets of parentheses out of n?” Since this is obviously nCr, we can see why these combination values show up as the binomial coefficients. But why do they show up in Pascal’s triangle?

    Psacal’s triangle begins with the top row containing two ‘1’s. Each subsequent row is built by starting and ending with a ‘1’ and obtaining the middle values by adding the two elements above it in the previous row. Hence, the second row starts and ends with ‘1’, with the middle ‘2’ being the sum of ‘1’ and ‘1’ from the first row, giving 1 2 1. The third row starts and ends with ‘1’, with the middle values of ‘3’ being the sum of 1 and 2 and the sum of 2 and 1 respectively, giving 1 3 3 1.

    We can see how this happens. We can write

    Now, to get the term with arbn – r, we need to either select a from the first parentheses and the ar – 1bn – r term from the second parentheses or select b from the first parentheses and the arbn – r – 1 term from the second parentheses. However, both ar – 1bn – r and arbn – r – 1 are terms from the (n – 1)th row of Pascal’s triangle, that is the preceding row.

    Moreover, the term with ar – 1bn – r is the rth element of the (n – 1)th row, while the term with arbn – r – 1 is the (r + 1)th element of the (n – 1)th row. And the term with arbn – r is the (r + 1)th element of the nth row.

    But this means that the (r + 1)th element of the nth row is the sum of the rth element of the (n – 1)th row and the (r + 1)th element of the (n – 1)th row, which is exactly how each subsequent row of Pascal’s triangle is built. We can put this in terms of combinations and write

    Since the above equation relating binomial coefficients indicates the way the elements of Pascal’s triangle are obtained, it is clear why the two are identical.

    Making it Count

    So far we have learned how to determine the number of permutations of r out of n distinct objects as well as the number of combinations of r out of n distinct objects. We have also seen how the binomial coefficients relate to the elements of Pascal’s triangle. We could have proved the final relation using algebra as below.

    However, the algebra does not give us any special insight, which is what we need. We did get some insight when we showed why Pascal’s triangle has elements that are the same as the binomial coefficients and when we showed why the binomial coefficients show how Pascal’s triangle is built up. But we have only just started our journey of learning how to count.

    In this post, we have considered permutations and combinations of distinct objects in a row. What if some of the objects are not distinct? What if the objects are not in a row, but in a circle? What if we have some restrictions, like two objects cannot be placed side by side or that two objects must always be placed side by side? How do we manage to use the basic counting principles to determine how to proceed counting in these cases? We will turn to that in the next post. Till then, permute your life to make every moment count.

  • Down for the Count

    What Are Counting Principles?

    (Source: Inner Drive)

    Counting is something that we learn from a very young age, either in the informal environment at home or in the formal environment of school. It forms the basis of all the mathematics we learn through our lives. All the basic mathematical operations (addition, subtraction, multiplication, division, and exponentiation) can be explained in terms of counting. Hence, it is often the case that, when students reach high school, after probably 10 years of formal mathematics, they are surprised when they see a chapter in their book with the title “Counting Principles”. They may think, “What principles might this involve? How much more is there to counting? Didn’t we put the issue of counting behind us when we learned how to perform the operations?”

    What the student does not realize is that what she has learned so far are ‘recipes’ for performing the mathematical operations. That is, she has been given some idea of what the operations involve. However, the main focus would have been on how to perform the operations not on why certain operations are needed to be performed. For example, if you were given 3 ⊗ 7, where ⊗ indicates some mathematical operation, what would the result be? 3 + 7 gives us 10, 3 – 7 would yield -4, 3 × 7 is 21, 3 ÷ 7 would be 0.428571…, and 37 is 2187. While the student would easily be able to determine each of these five answers, which operation should she use in a given context? This is where the idea of the counting principles comes in. These principles tell us which operations are to be used in a given context.

    The Multiplication and Addition Principles

    As an example, suppose a restaurant offers a 3-course lunch with 3 options of starters, 5 of main courses, and 2 of desserts. How many different selections of lunch can a customer make? Or if you have a choice of a room from 3 hotels, one of which has 20 rooms, the second 30 rooms, and the third 50 rooms, how many choices of rooms do you have? How do the 3, 5, and 2 in the first situation relate to each other. How do the 20, 30, and 50 in the second situation relate to each other? There needs to be some principles on the basis of which the student would decide how to find the answer to each of the situations. What are these principles?

    Today, we are starting a new series on counting principles. We will start with some basic ideas and work ourselves to more complex ideas. At the end we will answer the following question: “For a theatre production of a play there are n characters, each of which requires an understudy. If any of the actors and understudies can play all the parts and if the main actor must have more years of experience than the understudy, in how many ways can main actors and understudy actors be assigned?”

    As promised, let us begin with the two earlier examples, which are relatively easy. Suppose we label the starters as A, B, and C, the main courses as P, Q, R, S, and T, and the desserts as Y, and Z. The possible choices are listed below:

    In the above, each row represents a different choice of starter. The colors differentiate the main courses. Finally, the dessert choice is differentiated between normal and italicized fonts. We can see that there are 40 possible selections because 4 × 5 × 2 = 40. But the reason we multiply is that the customer has to choose a starter and a main course and a dessert.

    In the case of the hotels, we cannot multiply because the person can only occupy one room. Hence, he must choose to go to either hotel A, where he has a choice of 20 rooms, or hotel B, where he has a choice of 30 rooms, or hotel C, where he has a choice of 50 rooms, yielding a total of 20 + 30 + 50 = 100 choices.

    The situation with the lunch choices is one in which we use what is known as the multiplication principle, while the case with the hotel rooms uses the addition principle.

    The multiplication principle states that, if there are m ways of doing one thing and n ways of doing a second thing, then the number of ways of doing both things is m × n. The addition principles states that, if there are m ways of doing one thing and n ways of doing a second thing, then the number of ways of doing either thing is m + n.

    Since the lunch menu required a choice of starter and main course and dessert, the multiplication principle was applicable. And since the hotel room required a choice of only one of the three hotels, the addition principle was applicable.

    Your Turn

    Why don’t you try the questions below?

    1. A football squad consists of 3 goalkeepers and 5 strikers. In how many ways can the coach choose 1 goalkeeper and 1 striker?
    2. A library allows members to borrow two books at a time. The library has 15 books by Jeffrey Archer and 23 books by Paulo Coelho. In how many ways can a member borrow 1 book by each author?
    3. There are 5 apples and 7 oranges in a fruit basket. In how many ways can a person choose either an apple or an orange?
    4. A student has 3 colleges to choose from. The first college has 3 programs, the second has 5 and the third has 6. Assuming that the programs are full-time programs, in how many ways can she choose a program?
    5. A library allows members to borrow only one book at a time. The library has 15 books by Jeffrey Archer and 23 books by Paulo Coelho. In how many ways can a member borrow a book by either author?
    6. Three cities A,B, and C are connected by 4 roads between A and B, 5 between B and C, and 6 between C and A. In how many ways can a round trip be made?

    How did you fare with the above questions? The answers are 15, 345, 12, 14, 38, and 720. Many students get the first 5 but stumble on the last one. The answer I have given is correct. It is 720. If you wish to check the solution, click here.

    Checking Out

    As we continue with the series, we will see that there are many ways to put these two basic counting principles together. We will learn about permutations and combinations in the next post as well as the relation of the latter to Pascal’s triangle. We will also learn about how permutations and combinations relate to each other. We will also see why the combinations show up as the coefficients of the binomial expansion. Till then, let everything count.

  • Four Tangential Circles

    This will be the final post for 2025. And it is a short one. I will be taking a break of a few weeks after that and will resume on 16 January 2026. For this final post, I would like to consider another problem I recently came across, depicted in the figure below.

    Each of the four circles is tangential to the other three. Also, it is given that the radius of the largest circle is 2 units and the radii of the two identical circles is 1 unit. We are asked to determine the radius of the smallest circle.

    As is often the case with geometry problems, a few simple constructions and a properly labelled diagram prove to be immensely helpful. These are shown below.

    Here, A and B are the centers of the two identical circles and C is the center of the smallest circle. D is the point of tangency of the biggest and smallest circles. P is the point of tangency of the two identical circles. E is the point of tangency of the smallest circle and one of the identical circles. The points D, C, and P are collinear. Similarly, the points A, E, and C are collinear. Let the radius of the smallest circle be r.

    Now, we know that AP = 1. AC = AE + EC = 1 + r. And CP = DP – DC = 2 – r. We can simply use Pythagoras’ theorem to obtain (1 + r)2 = 12 + (2 – r)2. This is trivial to solve as it yields a linear equation that gives r = 2/3.

  • A Geometric Bifecta

    Problem 1: Pure geometry

    I recently came across two other interesting geometry problems, which I would like to tackle here. The first is depicted in the figure below.

    In the figure above, ΔABC is isosceles, with AB = AC and ∠A = 36°. Point X on side AB and point Y on side AC are chosen so that AX = BC = CY . Prove that BY and CX are perpendicular.

    Given that the measure of ∠A is specified exactly and that the triangle is said to be isosceles, we should expect that both those factors of the problem will feature in the solution. We begin by observing that, if ∠A = 36° and ΔABC is isosceles, it must follow that ∠B = ∠C = 72°. But as soon as we say that, we also realize that 36 is half of 72. Could it be the case that CX actually bisects ∠C? Let us attempt to approach this by assuming that CX does not bisect ∠C. In that case, there must be another point Z on AB such that CZ bisects ∠C. This is shown in the figure below.

    Now, if CZ bisects ∠C, then it follows that ∠ZCB = ∠ZCA = 36° = ∠A. Hence, in ΔZCA, ∠A = ∠ZCA, meaning that ΔZCA is isosceles, allowing us to conclude that CZ = AZ.

    Now, ∠BZC is an exterior angle of ΔZCA. This means that its measure is equal to the sum of the opposite angles. Hence, ∠BZC = ∠A + ∠ZCA = 36° + 36° = 72° = ∠B. Hence, in ΔBZC, ∠BZC =∠B, meaning that ΔBZC is isosceles, allowing us to conclude that CZ = BC.

    This means that AZ = BC. However, we are given that BC = AX. This can only be true if X and Z are the same point. Hence, we can conclude that CX bisects ∠C.

    However, we are also given that BC = CY. Hence, ΔBCY is isosceles. But CX bisects the apex angle of this isosceles triangle, which means that it must be perpendicular to the base BY. And this concludes the proof.

    Problem 2: Geometry and number theory

    The second problem is depicted in the figure below.

    In the figure above, the area of ΔABC is a whole number. Lines AX and BY are drawn, where X lies on side BC and Y lies on side AC, and these lines meet at point P, inside the triangle. The area of ΔBPX is 1, the area of ΔAPY is 2, and the area of ΔAPB is a whole number. Find the area of ΔABC, and prove that your answer is correct.

    We begin by drawing the line PC and by labelling the regions as shown in the figure below.

    Hence, the areas of ΔABP, ΔPXC and ΔPY C are m, s and t, respectively, as indicated in the diagram. By hypothesis, m is an integer, and hence s + t is an integer, which we will call n. The ratio CX/BX is equal to the ratio of the area of ΔACX to the area of ΔABX, since the two triangles have the same height. This ratio is also equal to the ratio of the area of ΔPCX to the area of ΔPBX for the same reason. Hence,

    Similarly, the ratio CY/AY is equal to the ratio of the area of ΔBCY to the area of ΔBAY, which is equal to the ratio of the area of ΔPCY to the area of ΔPAY. Hence,

    Now, since n = s + t, we can obtain

    Some basic algebraic manipulations will give us

    Now, since s + t = n is a whole number, we must have, n ≥ 1, which means that

    Rearranging this we get

    Since m is a whole number, we must have m is an element of the set {1, 2, 3, 4, 5}. The corresponding values of n are -10, 7, 18/7, 11/7, and 26/23. This means that the only solution is m = 2 and n = 7, allowing us to conclude that the area of ΔABC is 1 + 2 + 2 + 7 = 12.

  • Four Triangles, Three Squares, and One Hexagon

    Framing the Problem

    I recently came across an intriguing problem that I thought worth pursuing. It is represented by the figure below.

    We are given a triangle XYZ. On each of its sides, we construct a square so that the squares are outside the triangle. This gives us the squares XYCB, YZED, and ZXAF. Now, we join the segments AB, CD, and EF, thereby forming a hexagon ABCDEF. We have to show that the areas of ΔXYZ, ΔABX, ΔCDY, and ΔEFZ are equal.

    Note that this holds true for any initial ΔXYZ. Hence, we cannot assume anything special about the starting triangle. If you wish to explore this, you can access a Geogebra applet I created here. You can click and drag on X, Y, or Z to change the initial triangle. All the other points are automatically generated. You can convince yourself that the four triangles do indeed have the same area.

    The solution, once it strikes you, is really quite elegant and does not require making any tedious measurements. Measurements of any given situation of course would not constitute a proof of any kind. I cannot stress this point enough. So please allow me a short diversion while I vent about one particularly troubling issue. I will proceed with the solution after that.

    A Reason for Venting

    Mathematical proof is something that works quite differently from so-called ‘proofs’ in other areas of human knowledge. In mathematics, proof proceeds by deductive reasoning, while in every other field, what qualifies as ‘proof’ proceeds either by inductive or abductive reasoning. In The Promise and Pitfalls of Mathematical Abduction I had written in length about these modes of reasoning. The image below captures the essential differences between the three primary modes of reasoning quite well.

    Comparison between deductive, inductive, and abductive reasoning. (Source: Design Thinking)

    A Geometric Excursus

    Since the image above may be too general, let me reiterate the differences by taking a specific example. Suppose we are attempting to prove that the sum of the angles of a triangle is 180°. We could start with a particular triangle, like the one below.

    A quick scratch pad addition will confirm that the sum of the angles is 180°. We could proceed to another triangle shown below.

    Once again we can confirm that the sum of the angles is 180°. However, we have actually not proved anything! All we have done is confirm the hypothesis for two triangles. Note that the angles are different in the two triangles. Indeed, there are infinitely man values that could be chosen for angle A and for each of those infinitely many for angle B. Assuming the sum of the angles is 180°, choosing A and B would fix angle C since the sum is a constant. However, we have an infinite number of triangles. And no matter how many triangles we confirm the hypothesis for, there will always be infinitely many more triangles that remain untested.

    For example, there is the conjecture that the two numbers a = n19+ 6 and b = (n + 1)16 + 9 are relatively prime. However, you have to test till n = 1, 578, 270, 389, 554, 680, 057, 141, 787, 800, 241, 971, 645, 032, 008, 710, 129, 107, 338, 825, 798 (61 digits), before you reach a counterexample with the two numbers having a greatest common divisor equal to 5, 299, 875, 888, 670, 549, 565, 548, 724, 808, 121, 659, 894, 902, 032, 916, 925, 752, 559, 262, 837!1 We don’t even have names for numbers this large! In contrast, if the universe is 14 billion years old, that is only about 441, 504, 000, 000, 000, 000 seconds! That’s 441 trillion, 504 billion seconds. It’s nameable. My point is that there is no way to prove a conjecture like this by the method of testing since a single counterexample will disprove it and there is no guarantee if or when we will encounter the counterexample.

    However, we can prove the result for the sum of the angles of a triangle in a very elegant manner. Consider a general triangle as shown in the figure below.

    Now, we draw a line parallel to BC passing through A. This is shown below.

    Now since DE is parallel to BC, ∠DAB and ∠ABC are alternate interior angles and are, therefore, equal. By a similar argument, ∠EAC and ∠BCA are equal. Hence, ∠ABC + ∠CAB + ∠BCA = ∠DAC + ∠CAB + ∠EAC. However, ∠DAC, ∠CAB, and ∠EAC add to form a straight line, which by definition is 180°. Hence, we can conclude that the sum ∠ABC + ∠CAB + ∠BCA is 180°, thereby proving the result.

    What we have seen here is an example of deductive reasoning where we proceed from a general triangle to a result that is true about any specific triangle. This is the kind of reasoning mathematics engages in and I really wish my fellow mathematics teachers spent time teaching students the difference between ‘proof’ and ‘confirmation’ or ‘verification’.

    An Elegant Solution

    With that out of the way, we can return to our opening problem for which we will use one of the elements of the preceding proof. Let’s remind ourselves of our problem with the figure once again.

    Let us focus on ΔABX and ΔXYZ. If we can prove that they are equal in area, we can prove that all four triangles are equal in area because there is nothing special about ΔABX. We also observe that ∠BXY = ∠AXZ = 90° since they are interior angles of squares. What this means is that ∠AXB + ∠ZXY = 180° since the angles about a point equals 360°.

    We now proceed with the realization that moving an object does not change its size. Let us rotate ΔXYZ about vertex X in a counterclockwise direction until line XZ coincides with line XA. This will give us the figure below.

    Note that the point A is also the point Z’. However, to avoid confusion, let us refer to it as A. Now, since ∠AXB + ∠ZXY = 180°, it follows that ∠AXB + ∠AXY’ = 180° since rotating ΔXYZ does not change its internal angles. But this means that B, X, and Y’ form a straight line since the angle formed by a straight line is 180°. Further, X is the midpoint of BY’ since BX = XY’. Hence, X divides ΔABY’ into two equal halves. This means that the areas of ΔABX and ΔAXY’ are equal. But since rotating does not change the size of a triangle, this means that ΔABX and ΔXYZ are equal in area.

    What we have seen is that this problem can be solved quite elegantly with just the basics of school geometry. In fact, we have not used any geometric results that are taught beyond grade 10. In other words, any high school student should be able to understand the solution. However, what the solution required is a willingness to move things around. There are times when we need to break things down before we can put them together in ways that reveal more than conceal.

    1. I obtained this information from Math Stack Exchange. ↩︎

  • A Festival of Flipping Lights

    Presenting Problem

    (Source: The New York Times)

    I recently came across the following problem: Eight lamps, each with an on-off switch, are arranged in a circle. A lamplighter can flip (in other words, change the state of) the switches, but he is not allowed to flip just one at a time. When he switches lamps on or off, he is required to flip the switches of three consecutive lamps simultaneously. (For example, he can flip the switches of lamps G, H and A at the same time.) Prove that no matter what set of lamps was turned on at the start, the lamplighter can turn all the lamps on.

    Recognizing the Requirement

    Since we are entering the Christmas season, which is a season of lights, I wish to tackle this specific problem and then extend it to a more general situation. Now, since the final state of all the lights is the same with all being on is accomplished regardless of the initial state of the lights, it must mean that it is possible to change the state of any particular light after a finite number of moves. Then we can repeat the process as needed to change the state of every light that is currently off so that it is on. In effect this means that we are able to transform any starting pattern to any other desired pattern with a finite number of steps, each of which consists of flipping three switches.

    Initial Proof

    To begin with let us just assume that all the lights are off. This is shown in the figure below.

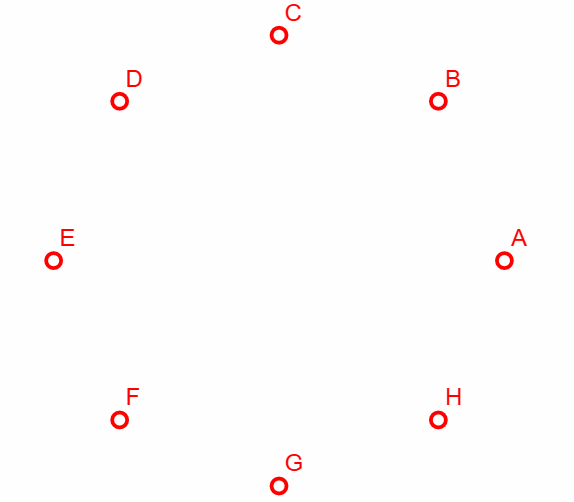
    Here, I am adopting the convention that a filled-in circle represents a light that is on. Hence, an empty circle is a light that is off. Now, the challenge is to use a finite number of moves to change the state of one and only one of the lights. Let us arbitrarily start at A. Hence, we have to flip the switches A, B, and C. This will give us

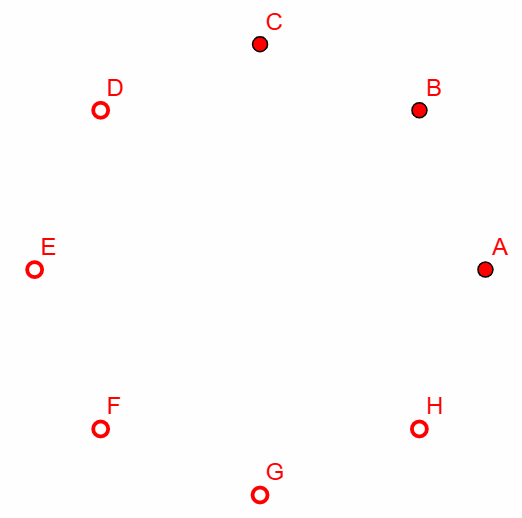
    Now, we can flip the switches D, E, and F to give us

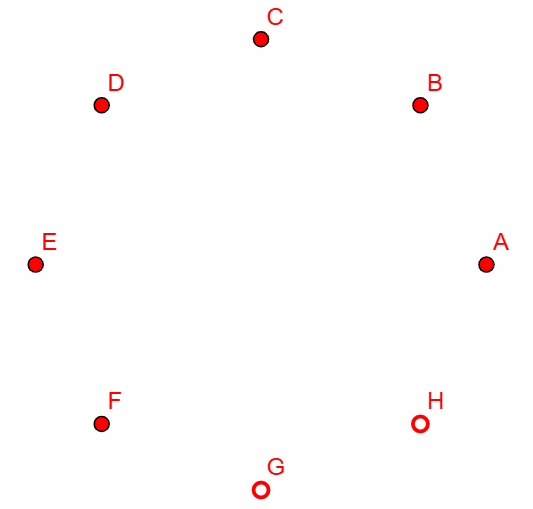
    Finally, we can flip the switches G, H, and A to give

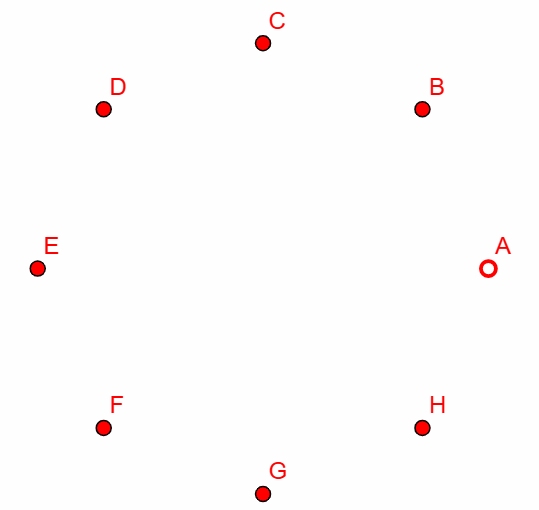
    We can see that, after three switching sets we have actually managed to alter the state of all the lights except A. If we continue this process, the next two outcomes will be:

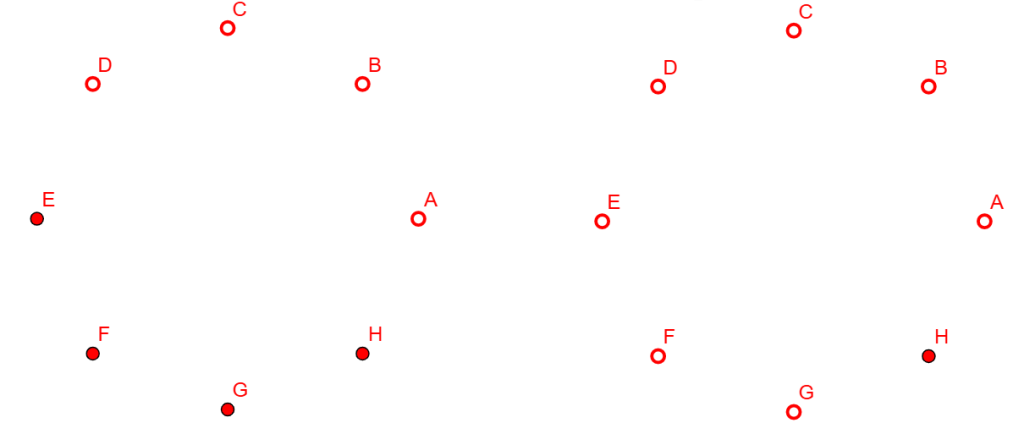
    Note that, starting with A, after 5 switching sets, we have managed to alter the state of only H. This is because, 5 switching sets involves 15 switching elements, which is 1 less than 2 times 8. Hence, all the lights from A to G get switched twice, restoring them to their original state, while H gets switched only once, thereby flipping its state. In other words, if I desire to flip the state of one of the lights, all I need to do is start with its successor and perform 5 switching sets. Let us test this on an example.

    Verification

    Since there are 256 (i.e. 28) different permutations of on and off lights in the set of 8, I used a random number generator to first choose a number from 1 to 256 and then iterated the random number generator that many times. The first number it spat out was 55 and I then generated 55 more numbers. This gave me 158, which in binary is 10011110. Hence, the starting case will be lights B, C, D, E, and H switched on. This is shown below.

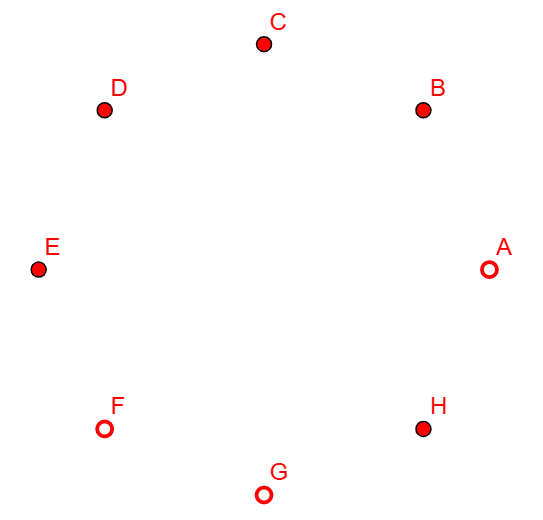
    We will represent this state as aBCDEfgH, where the lower case letters indicate that the light is switched off and the upper case letters indicate it is switched on. Hence, we have to switch the lights A, F, and G on to achieve our goal. We will start with B, which is the successor of A. Performing 5 sets of switching we obtain the following states:

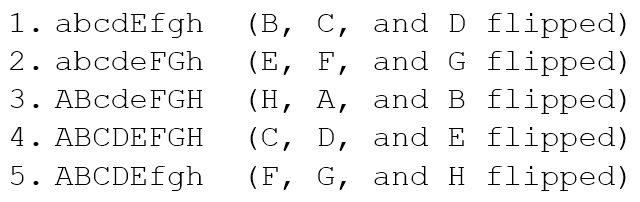
    Note that, even though the goal was to change the state of only A, which we manage in step 5 as expected, step 4 actually gives us the final state we wanted. For now, we will ignore any occasions when the final state is accomplished in the middle and proceed only with the state after 5 sets are complete. Hence, we will continue with the state ABCDEfgh. Now F needs to be flipped. So we start with G and the next 5 sets will give us

    Now, we need to flip G. So starting with H the next 5 sets give us

    So, we have managed to flip light G on as well, leaving only light H off. Now, we start with A and the next 5 sets will give us

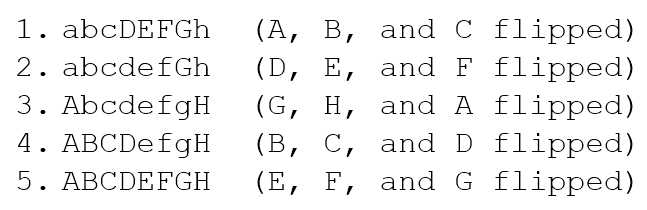
    We have, therefore, achieved the final state we wanted with all lights switched on. Note, that the initial state I chose was done at random. Indeed, our algorithm indicates that, starting with any particular light, after 5 sets of switching its predecessor will be the only one to have changed states.

    Bezout’s Identity

    Why does this happen? Is this limited to the numbers 8 (for number of lights) and 3 (for number of consecutive lights in each set)? Of course not! Rather, what we see here is the fact that

    Here, the ‘2’ indicates the number of times all except one of the lights have their states changed and the ‘5’ represents the number of sets that need to be performed to isolate one light and flip only its state. Is it possible to generalize this?

    Indeed it is! This is an example of an application of what is known as Bezout’s identity. Étienne Bézout was a French mathematician who did significant work on number theory. He demonstrated that, if a and b are two natural numbers, then there exist integers p and q such that

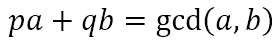
    In our example, a = 8 and b = 3, for which gcd(8, 3) = 1. Here we have found p = 2 and q = -5 such that

    Testing a Hypothesis

    We can readily see that the reason we were able to isolate one of the lights was precisely because 5 sets of 3 each put us 1 short of a multiple of 8. Hence, can we propose that if we choose a lights and restrict ourselves to flipping sets of b consecutive lights, where gcd(a, b) = 1, then we should be able to isolate any light by conducting q set flips, which will accomplish p changes of state to all but 1 light? Let us test this hypothesis with an example.

    Suppose now we have 11 lights and restrict ourselves to flipping 4 consecutive lights. Let us begin with the state abcdefghijk, where all the lights are off. We observe that

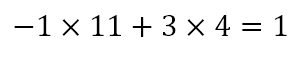
    Now, starting with A and performing 3 set flips, we will get

    We have indeed isolated light A. However, rather than flipping the state of only A, we have managed to flip the state of all lights except A! Can we rectify this? Of course, we can! Bezout’s identity does not say that the pair (p, q) is unique. Indeed, we can observe that

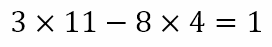
    This seems to indicate that we should be able to isolate A and change its state. When we perform 8 flip sets we will get the following.

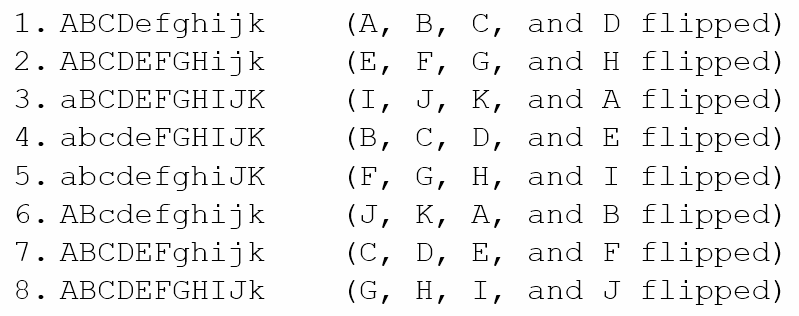
    Once again we observe that we have indeed isolated one of the lights, in this case K. And now too we have left it unflipped while flipping all the others. Are we stuck?

    Let us try to interpret the numbers in the equation

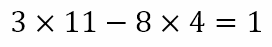
    The ’11’ and ‘4’ are clear. There are 11 lights and we are forced to flip 4 consecutive lights. The ‘8’ indicates that we will perform 8 flip sets. But the ‘3’ indicates that, when we have isolated one of the lights, all the others would have undergone ‘3’ state changes. Hence, all the lights, except the one we are focusing on actually change their states, leaving the one we are focusing on with an unchanged state. Hence, with 11 lights and flip sets of 4 consecutive lights it is not possible to isolate 1 light and change one its state. It is possible to leave only its state unchanged.

    Indeed, if 11p + 4q = 1 has to hold for integers p and q then it is necessary for p to be odd. However, p indicates the number of state changes that all lights other than the one we are focusing on undergo. This means that all the other lights will change states and the one we are focusing on remains unchanged.

    Modifying the Hypothesis

    For us to be able to isolate 1 light for a state change, it is necessary but not sufficient that ap + bq = 1. In addition, p must be even so that all other lights return to their original states while the light we are focusing on changes its state. However, from ap + bq = 1 we obtain

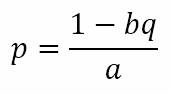
    If p is even, this means that both b and q must both be odd because only then can the difference 1 – bq be even. So let’s assume that a = 12 and b = 5. The GCD of 12 and 5 is 1. Will that allow us to isolate any particular light? From the above formula, we can see that

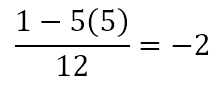
    Hence, with a = 12 lights and b = 5 being flipped each time, we should need q = 5 sets, each, except the one we start with, being flipped p = 2 times. Let’s test this starting with abcdefghijkl, the situation where all 12 lights are off. Carrying on with flip sets of 5, we can obtain the following

    As can be seen, we have isolated light A and changed only its state without affecting the states of any of the others. This will allow us to change any pattern to any other pattern we desire.

    Stringing Along

    What we have seen is that, if the number of lights is odd, then we are not guaranteed that there is a strategy that could convert any given pattern to any other pattern. However, if the number of lights is even and the number we flip each time is coprime with the number of lights then we may be to alter any starting pattern to any other pattern. However, this is not guaranteed. Is there a way of obtaining a generalized solution to this? That is, can we determine the exact conditions for a, the number of lights, and b, the number of lights flipped each time, that will always give us the possibility of changing any starting pattern to any other pattern?

  • Identifying Linear Commonalities

    The Final Spur

    For some weeks now, we have been focusing on the conic sections. In the last post, A Mathematical Straight Couple, we introduced the pair of lines as a degenerate hyperbola. We saw that the joint equation of a pair of lines through the origin is

    This kind of equation, where the sum of the powers of the variables in each term is the same and the constant term is zero is known as a homogeneous equation. However, the general second degree equation in two variables, which is

    is not a homogeneous equation. For this equation, in the previous post, we defined

    and we showed that if ∆ = 0 the general second degree equation in two variables represents a pair of lines. In this post, I wish to look at determining the point of intersection of a pair of lines described in the form of the general second degree equation in two variables and to look at another concept known as ‘homogenization’.

    Transformation of Coordinates

    Before we can determine the point of intersection of the two lines, we need to learn about transformation of coordinates. Suppose we have a point A(x, y) according to a previously defined set of rectangular axes. Now suppose we move the origin and the axes (with translation only, no rotation) to the point (p, q). It is evident that the coordinates of all points on the plane will change. Suppose the new coordinates of A are (X, Y). This is shown in the diagram below.


    From the diagram above it is clear that X = x – p and Y = y – q. Hence, when we move the axes p units to the right and q units up, the new x and y coordinates, indicated by capital letters in our convention, are reduced by p and q respectively.

    The Point of Intersection of the Lines ax2 + 2hxy + by2 + 2gx + 2fy + c = 0

    Suppose the equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents two straight lines and that their point of intersection is (p, q). Now, if we shift the origin to the point of intersection, we should get a homogeneous equation in the new coordinates because the lines now pass through the new origin. From what we know about transformation of coordinates X = x – p ⇒ x = X + p and y = Y + q. Making these substitutions we get

    Grouping terms according to degree and variable we get

    If this is a homogeneous equation it must reduce to

    Then we must have

    Now since (p, q) is the point of intersection of the lines, the coordinates must satisfy the joint equation of the lines. Hence,

    Hence, the third equation above is automatically satisfied by the point of intersection of the two lines. Solving the equations ap + hq + g = 0 and hp + bq + f = 0 simultaneously we get

    which gives the coordinates of the point of intersection.

    Coincident and Parallel Lines

    Recall, from the previous post, that the angle between the lines

    is given by

    It is clear that, if h2 – ab = 0, then the angle between the lines is 0°, meaning that the lines are either coincident or parallel. In that case, there will be infinitely many points common to the two lines or no points in common. Hence, we can say that, if ∆ = 0, h2 – ab = 0, bg – hf = 0, and af – gh = 0, then the lines are coincident. Also, if ∆ = 0, h2 – ab = 0 and either bg – hf ≠ 0 or af – gh ≠ 0, then the lines will be parallel.

    Homogenization of a Curve with a Line

    Suppose we have a curve S = ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 and a line L = lx + my – n = 0. These are shown in the figure below in red and green respectively.

    Let the line and the curve intersect at A and B as shown. It is evident that the coordinates of A and B satisfy the equations of both the curve and the line. Hence, A and B satisfy any combination of the two equations. Suppose we write the equation of the line as

    This is true for points A and B. Hence,

    holds at points A and B. Hence,

    However, this last equation is a second degree homogeneous equation in two variables and must represent two straight lines through the origin O that also pass though points A and B. Hence, this last equation represents the joint equation of the lines OA and OB.

    Now, the concept of homogenization might seem to be strange and perhaps even difficult to use. So, let us actually use it to solve a problem.

    Using Homogenization

    Let us prove that chords of the parabola y2 = 4ax which subtend a right angle at the origin pass through a fixed point. Note that what follows is a standard 4-step approach to problem solving, which I hope will help some of the readers since it works in pretty much every area of life and not just mathematics!

    Step 1: Information collection
    Given the parabola y2 = 4ax. Let the chord be lx + my – 1 = 0. We have to prove that if the chord subtends a right angle at the origin then it must pass through a fixed point.
     
    Step 2: Conceptual plan
    If we homogenize the equation of the curve S = y2 = 4ax with the equation of a line L = lx + my – 1 = 0 then we obtain the joint equation of the lines joining the origin to the points of intersection of the curve S and the line L. Further, the lines ax2 + 2hxy + by2 = 0 are at right angles to each other if a + b = 0.

    Step 3: Execution
    Homogenizing with the equation of the parabola we get

    This represents a pair of lines through the origin. If the lines are perpendicular to each other

    Hence, the line is

    where m is a parameter. This represents a family of lines all of which pass through the point of intersection of the lines x – 4a = 0 and y = 0. But the point of intersection of these two lines is (4a, 0). That is, the chord passes through the point (4a, 0)

    Step 4: Verification
    The working is correct and we have proved what had to be proved. And note that we did not even need to know that y2 = 4ax is a parabola!

    Journey’s End

    As we wrap up this series on the conic sections, we can observe that we have covered quite a bit of ground. We have looked at the geometric definition of a conic section as the curve formed when a cone is sectioned by a plane. We have also defined it in terms of coordinate geometry, using the focus, directrix, and eccentricity. We have derived the equations for the conic sections in standard form and have also derived the parametric coordinates of any point on the conic section. We have obtained the equations of the tangents at a point on the conic section in terms of Cartesian coordinates and parametric coordinates. We also introduced the idea of the chord of contact, the pole, and polar of a point in relation to a conic section.

    Along the way, we introduced the idea of degeneracy for a conic section and saw that the circle was a degenerate ellipse with eccentricity of zero. I defended the idea of including the pair of lines among the conic sections as a degenerate hyperbola with an infinite eccentricity. In this context, we looked at the conditions under which the general second degree equation in two variables represents a pair of lines. Then we obtained the point of intersection of a pair of lines and conditions for perpendicularity and parallelism of a pair of lines. Finally, we looked at the idea of homogenization, which we used to prove an important property of the parabola.

    Unfortunately, our journey into the world of the conic sections has come to an end. I hope it has been as enjoyable for you as it has been for me. I will be taking a break for a week and will resume on 5 December 2025. Till then, stay eccentric!

  • A Mathematical Straight Couple

    Making the Case

    We are in the middle of a series of posts on conic sections. After the introductory post, Finding Refreshment in the Desert, I devoted three posts to the circle and two each to the parabola, ellipse, and hyperbola. In the previous post I had mentioned a degenerate conic section known as a pair of lines. I know this doesn’t have the same kind of ring to it as do the others. But then, this is a degenerate conic section we are talking about. Many mathematicians do not consider it legitimate to include it among the regular conic sections. However, if we have included the circle, which is a degenerate ellipse, then I do not see why a degenerate hyperbola should not be included! Further, if a conic section is the curve obtained by sectioning a cone with a plane, then we can easily recognize that sectioning the cone through its apex will yield a shape that is actually two lines that intersect at the apex. Hence, I hold the view that the pair of lines is a valid conic section and should be studied under that umbrella.

    Joint Equation of Lines Through the Origin

    Our study of the pair of lines begins with a single line through the origin. Its equation will be y = mx. This means that m = y/x, which gives us the slope/gradient on the line. We can also write this as y – mx = 0. Any point on the line will satisfy its equation. We make the following observations: 1. the line passes through the origin; 2. the slope/gradient of the line is m.

    Now consider two lines y – m1x = 0 and y – m2x = 0. Let us consider the equation (y – m1x)(y – m2x) = 0. The represents the product of two numbers given by y – m1x and y – m2x. The equation states that this product is zero. However, the product of numbers can be zero if and only if one of the numbers is zero. This must mean that either y – m1x = 0, meaning that we have a point on the first line, or y – m2x = 0, meaning that we have a point on the second line. In other words the equation (y – m1x)(y – m2x) = 0 represents points that lie on either of the two constitutive lines. We call this equation the joint equation of the lines.

    If we expand the product, we will obtain a second degree equation that has the form

    If we divide this equation by x2, we will obtain

    Now recall that m = y/x. Hence, replacing y/x with m we get

    This is a quadratic equation in m and should have two solutions m1 and m2. From what we know about the sum and product of the roots of quadratic equations, these solutions satisfy the two equations

    So we have y/x = m1 or y/x = m2, both of which are straight lines through the origin. It follows that every second degree homogeneous equation in two variables represents the joint equation of two straight lines through the origin.

    Angle between the Lines ax2 + 2hxy + by2 = 0

    Let the lines make angles of θ1 and θ2 with the positive x-axis. Then m1 = tan⁡ θ1 and m2 = tan⁡ θ2, where

    If θ is the acute angle between the lines then

    Now, we know that

    Using the equations for the sum and product of the slopes/gradients we get

    Nature of the lines ax2 + 2hxy + by2 = 0

    We just derived

    From this we can conclude that, if h2 – ab > 0, we have two real and distinct lines, if h2 – ab = 0, we have two real and coincident lines, and if h2 – ab < 0, we have two imaginary and distinct lines. Further, if a + b = 0, we have two real and distinct perpendicular lines. It is crucial to note that in all cases the two lines pass through the origin – a real point! This is because zero is both real and imaginary!

    Joint Equation of General Pair of Lines

    Of course, we have only considered lines through the origin. What about lines in general? Let us consider the two lines

    Let P(α, β) be a point on either of the lines. Then either

    This means that the product

    Hence, the equation

    represents points that lie on either of the two lines. In other words, it is the joint equation of the two lines. Expanding the brackets we get

    This is of the form

    which is a general second degree equation in two variables. However, while this means that the joint equation of two lines is always a second degree equation in two variables, it does not mean that every general second degree equation in two variables represents a pair of lines.

    Now recall, from Finding Refreshment in the Desert, that the general second degree equation in two variables was obtained by sectioning a cone with a plane. If the pair of lines is a genuine conic section, then its equation should also satisfy the condition of being a general second degree equation in two variables. Of course, the equation

    satisfies the condition with g = f = c = 0. However, this represents only straight lines through the origin. What about straight lines that do not pass through the origin?

    If the general second degree equation in two variables represents a pair of lines then the LHS of the equation can be factorized into two linear factors. If we treat the equation as a quadratic equation in x we obtain the solutions for x as

    If we have two linear factors then the quantity under the root must be a perfect square. The quantity under the root is

    For this to be a perfect square, its discriminant should be zero. Hence,

    When the above condition is satisfied, the general second degree equation in two variables represents a pair of lines. Hence, we can conclude that the pair of lines is a genuine conic section since the general equation representing a conic section under certain conditions represents a pair of lines. What about when the condition is not satisfied? What can we say then?

    Conditions on ∆ and h2 – ab

    Let us define

    We have seen that, when ∆ = 0 the general second degree equation in two variables represents a pair of lines. We also saw earlier, the conditions for real and imaginary pairs of lines. We can collate this along with what we know about the other conic sections to obtain the table below.

    Of course, it will not do for me to just give you the final conclusions. We have derived the conditions for ∆ in this post. However, the conditions for the other conic sections can also be derived. Since this does not directly relate to the pair of lines, and because the derivation involves some serious algebraic juggling, those who are curious can view the derivation here.

    The Way Ahead

    I think in this post I have made the case for considering the pair of lines as a genuine conic section. I do not know why they are often excluded from the study. However, if the circle, which is a degenerate ellipse with eccentricity of zero, is included, why should the pair of lines, which is a degenerate hyperbola with and infinitely large eccentricity, be excluded? I think it is only because we are familiar with the circle from early years in school and are never taught to consider multiple lines together without aiming to solve them simultaneously to obtain their points of intersection. And since that is something that is often taught, in the next post we will consider how to use the general second degree equation in two variables to obtain the point of intersection (if it exists) of the two lines. We will also look at a procedure known as homogenization. Curious? Stay tuned!